Oblicz pole koła wpisanego w trapez. N.: W trapez równoramienny o podstawach długości a i b można wpisać koło. Oblicz pole tego koła.

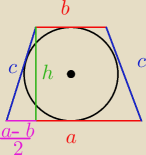
Saizou : a+b=2c (bo koło wpisane w trapez) założenie a>b

a+b
	=c
2

z tw. Pitagorasa

	a−b
h2+(		)2=c2
	2

	a−b		a+b
h2+(		)2=(		)2
	2		2

	a+b		a−b
h2=(		)2 −(		)2
	2		2

	a+b+a−b		a+b−a+b
h2=(		)(		)
	2		2

h²=ab h=√ab

	(a+b)h		(a+b)√ab
Pt=		=
	2		2

Mila: Trzeba obliczyc pole koła. h=2r

pigor: ... niech c− długość ramion trapezu, h − dł. wysokości trapezu, a>b, to z tw. o okręgu wpisanym w czworokąt i warunków zadania pole trapezu: (*) P_t= ¹₂(a+b)*h=? i 2c=a+b ⇒ h²= c²− (¹₂(a−b))² ⇒ ⇒ h²= (¹₂(a+b))²− (¹₂(a−b))² = ¹₄(a+b−a+b)(a+b+a−b) ⇒ ⇒ h²=¹₄*2b*2a= ab ⇒ h=√ab , zatem z (*) P_t= ¹₂(a+b)√ab − szukane pole trapezu. ...

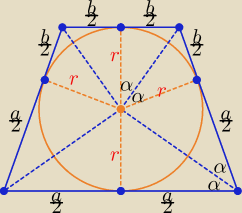
Bogdan: szkic:

	a		b		1
r2 =		*		, pole koła = πr2 =		abπ
	2		2		4

pigor: ... ale jaja pole koła ; więc r=¹₂h= ¹₂√ab , zatem P_k= π r²= ¹₄πab . ...

Saizou : faktycznie, trzeba było obliczyć pole koła a nie trapezu hehehe niedoczytanie

N.: No widzicie, też na początku liczyłam pole trapezu