dowód arli28: Długości boków równoległoboku wynoszą a i b, a długości jego przekątnych m i n. Udowodnij, że a⁴ + b⁴ = m²*n² wtedy i tylko wtedy, gdy kąt ostry równoległoboku ma miarę 45^o.

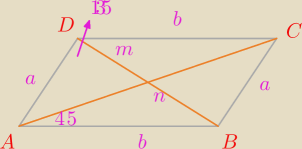
Lukas: ∡A=45^o ∡D=135^o m²=a²+b²−2abcos45^o n²=a²+b²−2abcos135^o m²=a²+b²−√2ab n²=a²+b²+√2ab Dodajemy stronami m²+n²=2a²+2b²

pigor: ... . chęci to miałeś dobre, ale to nie o to tu chodzi ...

Lukas: to nie wiem jak to zrobić ?

pigor: ..., a więc mnożąc stronami równania Lukasa : m²*n²= (a²+b²)²−2a²b² ⇔ a⁴+b⁴= m²n² . ...c. n.w. .

arli28: Dzięki

No name: no ja bym to trochę zmienił tam gdzie na rysunku jest 45 zmieniam na x i dalej tak jak pigor mówił, czyli mnożymymy m²*n²=(a²+b²−2abcosx)(a²+b²+2abcosx)). Mi wychodzi m²*n²=a⁴+b⁴+2a²b²(1−2cosx) i stąd 1−2cosx musi być równe zero czyli x=45

asdf: wydaje mi się, że powinno być m²*n²=a⁴+b⁴+2a²b²(1−2cos²x), czyli (1−2cos²x)=0 i x∊(π;π/2)

SEBA: Dokładnie, mamy udowodnić, ze jest kąt 45 stopni i tylko on spełnia te równanie.