stereometria arli28: Wyznacz objętość czworościanu, którego 5 krawędzi ma długość 2, a szósta ma długość √6.

Mila: Podpowiedź. "Postaw" ostrosłup na ΔABC o bokach : 2,2,√6, wtedy krawędzie boczne będą równe⇔ spodek wysokości ostrosłupa leży w środku okręgu opisanego na podstawie. Oblicz R i potem H z tw. Pitagorasa. Postaraj sie rozwiązać samodzielnie. Jaki wynik? Będę liczyc.

arli28: V=1. Nie wychodzi mi wynik, tak robiłam

PW: Cały kłopot to sporządzić dobry rysunek. Na płaszczyźnie kładziemy trójkąt ABC o bokach 2, 2, √6. Niech |AC| = √6 Trójkąt taki istnieje, bo 2+2 > √6. Pionowo stawiamy teraz trójkąt ACD − przystający do ACB. Po połączeniu B z D widzimy czworościan, w którym cztery krawędzie mają długość 2 i jedna ma długość √5. Niestety krawędź BD jest za długa − ma długość 5 > 2. Długość tę łatwo obliczyć z twierdzenia Pitagorasa − wysokości trójkątów ACB i ACD opuszczone na AC mają długości

	5
h = √		,
	2

a więc − jeżeli trójkąt ACD stoi prostopadle do płaszczyzny podstawy, to |AD|² = h²+h² = 5. Skoro w takiej pozycji krawędź AD jest za długa, to należy trójkąt ACD nachylić. Jaki ma być ten kąt nachylenia, żeby w trójkąt o bokach h, h, AD było |AD| = 2 ? Jeżeli to rozstrzygniesz, to i rysunek dobrze narysujesz, i obliczenie wysokości czworościanu nie będzie trudne.

PW: O, widzę, że mamy z Milą podobną koncepcje, tylko ja nie mówię o środku okręgu opisanego.

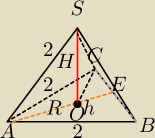
Mila: Wychodzi 1. W ΔABE: BC=√6

	√6
h2+(		)2=22
	2

	√5
h=
	√2

	1		√5		√30		√15
PΔABC=		√6*		=		=
	2		√2		2*√2		2

a*b*c		√15
	=
4R		2

	2√10
R=
	5

	2√10
(		)2+H2=22
	5

	√12
H=
	√5

	1	√15		√12		1		1
V=			*		=		*√36=		*6=1
	3	2		√5		6		6

pigor: ... , za podstawę weź sobie Δ o bokach 5,5,√6, wtedy krawędzie boczne maja długości po 5 i spodek wysokości H względem tej podstawy to środek okręgu opisanego na podstawie (rzuty prostokątne krawędzi bocznych na podstawę to promienie R tego okręgu) , a V=¹₃S*H=? , gdzie H²= 5²−R² , S − pole podstawy = ¹₂5²sinα , gdzie np. z tw. sinusów

	√6		5
2R=		=		⇒ 5*2cosα= √6 ⇒ cosα=0,1√6 ⇒ sinα=0,1√94
	sin2α		sinα

	5
więc S=58√94 , a 2R=		⇒
	0.1√94

	25		25		69		√69
⇒ R=		i H2 25−25*		=25*		⇒ H= 5		,
	√94		94		94		√94

zatem

	√69
V= 13*58√94*5		=2524√69 − szukana objętość.
	√94

ale nie ręczę za ... wynik . ..

pigor: ... , kurde, a ja "widziałem" długości po 5 , zamiast 5 po 2 ; przepraszam

PW: pigor, miało być 2, 2, √6, a nie 5, 5, √6

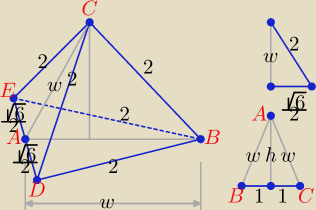
Bogdan: albo tak:

	1		√6
w = √4 − 6/4 =		√10, h = √w2 − 12 =		,
	2		2

	√6
pole trójkata ABC jest równe h*1 =
	2

Mamy tu dwa czworościany o wspólnej podstawie ABC, pierwszy ma wysokość AD,

	1
drugi ma wysokość AE, każda z nich ma długość		√6.
	2

	1		√6		√6
Objętość czworościanu EDBC jest więc równa 2*		*		*		= 1
	3		2		2

Kacper: Na co komu tyle rozwiązań?

Bogdan: Jak słyszałem, jesteś Kacprze początkującym nauczycielem. Bedziesz więc oceniał rozwiązania wielu osób, dostrzegał i oceniał sposób ich prezentacji i drogę dojścia do wyniku. Tutaj staram się pokazywać rozwiązania najmniej pracochłonne i alternatywne do już pokazanych.

Kacper: Prawdę mówiąc to chciałem mieć zapamiętany temat z moim imieniem i dlatego to napisałem

Bogdan: A przede wszystkim dobry wieczór . W dzisiejszym numerze mojego ulubionego pisemka "Komputer Świat", który kupuję od nr 1, znajduje sie na stronie 70 informacja polecająca uczniom serwis z − jak piszą, sporą bazą zadań wraz z roawiązaniami, czyli serwis matematyka.pisz.pl. Odczulem dużą przyjemność i satysfakcję po przeczytaniu tej notki i gratuluję Jakubie Tobie tego sukcesu, a także wszystkim osobom tworzącym ten serwis

Kacper: dobry wieczór To rzeczywiście wyróżnienie

arli28: dzięki

Jakub: Późno, bo późno, ale dziękuję Bogdan za informację. Kupiłem sobie ten numer na pamiątkę. https://matematykaszkolna.pl/forum/1.jpg https://matematykaszkolna.pl/forum/2.jpg

Bogdan: