Pole ogr.krzywymi Desperat.: Oblicz pole ograniczone dwiema krzywymi: y= √x i y=x. Jak to rozwiązać?

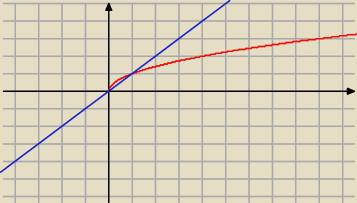
5-latek: Masz wykresy tych funkcji Teraz wedlug mnie nalezaloby obliczyc pukty przciecia sie tych wykresow √x=x dla x>=0 i idla x z prawej strony tez x>=0 Masz obie strony nieujemne wiec mozesz je podniesc do kwadratu x=x² to −x*2+x=0 to x²−x=0 to x(x−1)=0 to x=0 lub x=1 Masz punkty przeciecia ale calke musisz sobie obliczyc sam ( nie pamietam )

Desperat.: Właśnie tego mi tu brakowało Dziękuję ślicznie

5-latek:

Desperat.: A wie jak ktoś rozwiązać całkę? Wychodzi mi wynik ujemny...

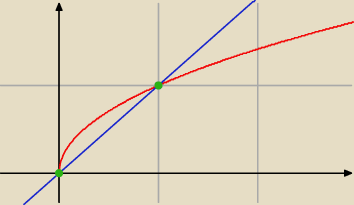
Saizou : tak jak mówi 5−latek liczymy punkt przecięcia się funkcji x=√x /² bo x≥0 x²−x=0 x=0 lub x=1 1 1

	2		1
∫ √x dx − ∫ x dx =		−		=...czy jakoś tak
	3		2

0 0

Desperat.: Ale wyżej jest funkcja y=x a nie y=√x ... Nie powinno być więc na odwrót?

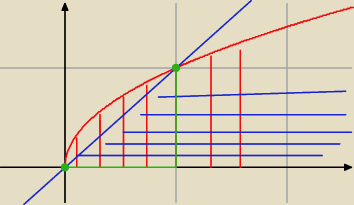
Saizou : jak myślisz, co trzeba odjąc ?

Desperat.: Czyli w takim razie ktoś źle mi wytłumaczył. Mam patrzeć na funkcję, która jest wyżej w wyższym punkcie? W tym wypadku w punkcie 1 wyższa jest y=√2. I to od tej funkcji odejmuje y=x.

Saizou : na przedziale [0:1] funkcja √x jest wyżej niż x

Desperat.: Mhm, teraz rozumiem Dziękuję za wsparcie

daras: denacie vel [P[Desperacie] całeczkę liczy się prościutko:

	1
∫√xdx − ∫xdx |10 =		> 0
	6

daras: wyższa/niższa po prostu pole liczone za pomocą całki to ZAWSZE pole pod wykresem funkcji aż do osi OX wiec żeby obliczyć pole obszaru pomiędzy musisz odjąć od większego pola to mniejsze ..ale to chyba już wiesz