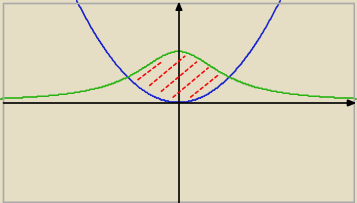
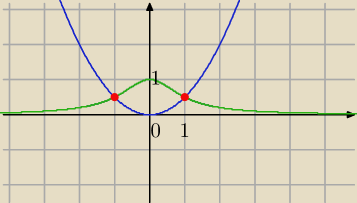
Obliczyć całkę i pole. Jaaa: Proszę o pomoc w obliczeniu całki z zadania: Oblicz pole obszaru D ograniczonego krzywymi y=1/(1=x²) ; y=²/2 Rysunek tak jak wyżej. Niebieską linią jest wykres x²/2 a zieloną 1/(1+x²). Pole oczywiście czerwone. Przedział jest o −1 do 1. I mam tak: D=∫[1/(1+x²) − x²/2] w przedziale od −1 do 1. Na początku zabrałem się za samo liczenie całki nieoznaczonej w czym się pogubiłem: ∫[1/(1+x²) − x²/2]dx = ∫1/1+x²dx − ∫x²/2dx = 1/2∫1/t dt − 1/2∫x²dx = 1/2 * ln|1+x²| − 1/2 * 1/3x² +C I teraz się zastanawiam czy mogę to zapisać w ten sposób: 1/2(ln|1+x² − 1/3x³), gdyż jak tak policzyłem to pole wyszło mi zero i teraz nie wiem czy to oznacza że to zadanie nie ma rozwiązania czy ja coś zrobiłem źle. Za pierwszym razem jak liczyłem to nie wyciągnąłem tak 1/2 przed nawias i pole wyszło mi na minusie.

Jaaa: No i teraz policzyłem i znowu mi coś nie wychodzi... Proszę o pomoc

PW:

	1
Całka z		to nie jest logarytm.
	1+x2

Jaaa: Taak wiem, ale ja tą całkę wyznaczyłem przez części czyli wziąłem za 1+x² podstawiłem t więc miałem 1/t dt wyznaczyłem całkę czyli ln|t| i podstawiłem z powrotem 1+x²

Jaaa: Tzn przed podstawianie nie przez części...

PW: Zajrzyj do wzorów.

Jaaa: No jest 1/x = lnx + C, ale teraz zauważyłem że jest wzór dx/(x²+c) gdzie c>0. Rozumiem że mam z niego skorzystać... Zaraz to przeliczę.

Jaaa: Dobra wyszło mi 49 i 2/3 j² . Poprawnie? Martwiło mnie trochę, że było dzielenie przez zero ale tam gdzie był nadmiar zer to powstawiałem po prostu 0 jako wyniki.

Jaaa: ? ? ?

Mila:

	1
f(x)=
	x2+1

	1
g(x}=		x2 obydwie funkcje są parzyste
	2

	1		x2
P=2*0∫1(		−		) dx=...
	x2+1		2

Obliczam całkę nieoznaczoną:

	1		x2
2*(∫(		dx−∫		dx)=
	x2+1		2

	1
=2*(arctgx−		x3)
	6

	1		1		π		1
P=2*(arctg1−		−arctg0+		*0)=2*(		−		)=
	6		6		4		6

	π		1
P=		−
	2		3

PW: A czy nie martwi Cię wynik? toż gdyby wziął tego pola więcej − taki prostokąt o wysokości 1, to pole byłoby na pewno mniejsze niż 49. Funkcje są symetryczne wzgledem osi OY − policz całkę na przedziale od zera do ... (czy dobrze wyznaczyłeś odciętą x₀ punktu, w którym przecinają się wykresy?):

	1		x2
		=
	x2+1		2

PW: Dobrze, niepotrzebnie pytam.

Jaaa: No wynik w sumie mnie martwi że taki duży bo w sumie 49 jednostek kwadratowych to dużo... Dobrze jeszcze raz to spróbuję przeliczyć i sprawdzę.

Jaaa: Przepraszam za zwłokę ale się zająłem innymi oblicenia bo myślałem, że się nie doczekam już tutaj odpowiedzi...

Jaaa: Aaaah może dlatego mi dziwnie wyszło bo ja ten acrtg policzyem na kalkulatorze i mi wyszło 50, w ogóle nie pomyślałem, żeby odczytać z tabelki... Aaagh... Już zaraz to zmienię.

Jaaa: Miła tylko tak się zastanawiam czemu zrobiłaś przedział od 0 do 1 skoro całe pole jest od −1 do 1... I skąd te 2* całka?

Jaaa: Przepraszam jeśli zadaję głupie pytania ale siedzę nad tym wszystkim już trochę i mnie już głowa boli przez to wszystko...

Jaaa: Aha bo liczysz funkcję od początku układu czyli od zera i że są dwie to 2 razy czy dobrze zrozumiałem

Jaaa: Ale czy druga wtedy nie była by od −1 do 0?...

Mila: Przecież tam jest symetria. Liczysz pole połowy "łezki", bo tak jest wygodniej i mnozysz przez dwa.

Jaaa: A co do miejsca przecięcia wykresów to jestem pewien że jest dobrze. Bo robiłem to wszystko tradycyjną metodą czyli tabelka i podstawiałem wartości. Także musi być dobrze bo sprawdzałem kilka razy i nawet na kalkulatorze liczyłem.

Jaaa: Ok czyli dobrze zrozumiałem skąd te razy 2.

Jaaa: Dobra chyba już zaczynam pomału rozumieć to zadanie... : )

Mila: To na koniec dyskusji pisze się dziękuję.

Jaaa: Tzn nie pisałem bo zastanawiałem się czy o coś jeszcze nie poprosić...

Jaaa: odnośnie tego. Ale teraz widzę, że już wszystko jest jasne. Także dziękuję bardzo wam obojgu za pomoc

Mila: