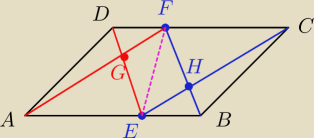
dowód arli28: Dany jest równoległobok ABCD oraz dowolne punkty E i F odpowiednio na bokach AB i CD. Odcinki FB i CE przecinają się w punkcie H. Odcinki AF i ED przecinają się w punkcie G. Uzasadnij, że pole czworokąta GEHF jest równe sumie pól trójkątów AGD i HBC.

Janek191:

arli28: I tylko tyle? A skąd wiesz, że np. AG=GE?

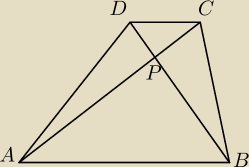
Saizou : takie coś sobie udowodnij Udowodnij że jeśli czworokąt ABCD jest trapezem (gdzie AB II CD) i punkt P jest punktem przecięcia się przekątnych tego trapezu to P_ADP=P_BCP

Janek191: @arti28; Skorzystaj z podpowiedzi Saizou i dowód natychmiastowy

arli28: jasne, teraz widzę

asiunia: Ja udowodniłam to w taki sposób, troche dłuższy, ale działa. Teza: P_GEHF = P_AGD + P_HBC Tak orientacyjnie, narysowałam sobie gdzieś wysokość h. Używając h mam wzór na pole całkowite P_c= h|AB| = h|CD| i dalej piszę tak: |AE| + |EB| = |AB| ⇒ ______________

	1		1		1		1
PABF=		|AB|h =		Pc =		|AE|h +		|EB|h = PADF+PFCB
	2		2		2		2

|DF| + |FC| = |CD| ⇒ ______________

	1		1		1		1
PCED=		|CD|h =		Pc =		|DF|h +		|FC|h = PADE+PEBC
	2		2		2		2

P_FCB+P_EBC−P_HCB + P_ADF+P_ADE−P_AGD = P_ABF+P_CED−P_GEHF

1		1		1		1
	Pc +		Pc − PHCB − PAGD =		Pc +		Pc − PGEHF
2		2		2		2

	1
skracam		Pc po obu stronach równania i zostaje mi:
	2

P_GEHF = P_HCB + P_AGD czyli moja teza