stozek abc: Wyznacz kat rozwarcia stozka wiedzac ze istnieja 3 parami prostopadle do siebie tworzace stozka.

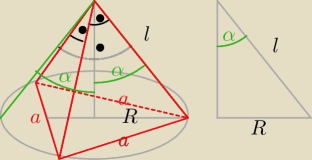
Bogdan: Ostrosłup prawidłowy trójkątny, krawędzie boczne mają długość l, kąt płaski przy wierzchołku ostrosłupa jest prosty. Ściany boczne ostrosłupa są trójkatami prostokątnymi o przyprostokątnych długości l i przeciwprostokątnej a. Stożek jest opisany na tym ostrosłupie. i − długość tworzącej, 2α − miara kata rozwarcia stożka

	1		1		1
a = l*√2, R =		a√3 =		*l*√2*√3 =		*l*√6
	3		3		3

	R
sinα =		= ... ⇒ α = ... ⇒ 2α = ...
	l

Kacper: Interesujące

abc: dzieki

PW: Bardzo ciekawe zadanie, dla mnie − jako człowieka pozbawionego wyobraźni przestrzennej − głównie z powodu trudności ze sporządzeniem rysunku. Dla humoru opiszę jak w moim wykonaniu wygląda taki „proces myślowy”. − Trzy prostopadłe do siebie jednakowej długości odcinki? Gdzie ja coś takiego widziałem? Tak! Trzy krawędzie sześcianu wychodzące z jednego wierzchołka. Rysuję sześcian. Tworzące stożka wymienione w zadaniu już widzę. − Gdzie będzie podstawa stożka? Trzy końce tych krawędzi wyznaczają płaszczyznę podstawy (przez każde trzy niewspółliniowe punkty przechodzi dokładnie jedna płaszczyzna. Trudno teraz narysować kółko w tej płaszczyźnie. Ułamuję pozostałe krawędzie sześcianu i stawiam te trzy na kartce. Patrzę na to z góry. Stożek to kółko z zaznaczonym środkiem. Rozważane trzy krawędzie to trzy promienie − widzę „pacyfkę”. Łączę parami końce promieni i nareszcie widzę w rzucie z góry − stożek z wpisanym ostrosłupem trójkątnym. Reszta już łatwa do policzenia, stosunki odcinków biorą się z sześcianu. Mateńko! Czy ja się muszę tak męczyć? A Bogdan usiadł i narysował zazdroszczę mu.

Mila: PW, Twoje rozumowanie też piękne.

pigor: ..., no cóż, Drogi PW piszesz że nie masz wyobraźni przestrzennej, może i tak, a może ci się tylko tak wydaje, bo dla mnie masz za to coś więcej, co nie jeden może Ci zazdrościć, a ja nie wstydzę się być tym pierwszym z nich .

abc: zadanie 2. Prosta laczaca srodki skosnych krawedzi czworoscianu foremnego o krawedzi dlugosci a jest osia walca. Podstawy walca sastyczne do czworoscianu w ich srodkach. Wyznacz objetosc walca.

abc: H(os walca) wyznaczylem jako pierwiastek z 2/3 wysokoci podstawy i polowy wysoosci czworoscianu, a dlugosc promienia mysle, ze bedzie to 1/3 wysokosc walca, skoro jest styczna. Ale wynik sie nie pokrywa z odp.

abc: ref

abc: up

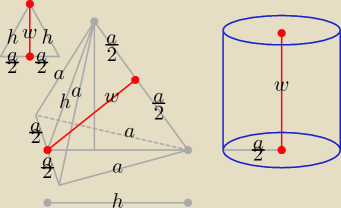
Bogdan: Cytuję treść zadania podanego przez abc 31 sierpnia o godz. 18:01. Prosta łącząca środki skośnych krawędzi czworościanu foremnego o krawedzi długosci a jest osią walca. Podstawy walca są styczne do czworościanu w ich środkach. Wyznacz objętość walca. Szkic rozwiązania:

	a√3		a
h =		, w = √ h2 − (a/2)2 =		, objętość walca V = ...
	2		√2

abc: Dziek, strasznie latwe to sie teraz wydaje. Teraz sie wkurzylem, ze odswiezalem temat zamiast sprobowac jeszcze raz to zrobic. Dzieki Bogdan jeszcze raz, sprawdzalem wynik jednego zadania w necie i wpadlem na twoj post/rozwiazanie z przed kilku lat. Musze tez pochwalic twoje rysunki, zawsze wszystko z nich widac

Bogdan:

Ben Akiba: wszystko już było rzekł Ben Akiba, a co nie było można sobie wyguglać wystarczy wpisać treść zadania w wyszukiwarkę i nie odkrywać na nowo Ameryki

Anna: Narysuj rzut

Krzysiek: