Przekształcenia prostej 123: Napisz równanie obrazu prostej l: 2x−3y+1=0 w przekształceniach: a) translacji o wektor u=[−3;2] b) symetrii względem prostej x=−3 c) symetrii środkowej o środku K=(1;−2) proszę o jasne wytłumaczenie

daras: http://www.google.pl/cse?cx=partner-pub-8082496537969329%3Amqxxzmak47q&ie=UTF-8&q=obraz+prostej+w&sa=Szukaj&siteurl=matematyka.pisz.pl%2Fstrona%2Fszukaj.html&ref=matematyka.pisz.pl%2Fstrona%2F3423.html&ss=3739j1147593j15#gsc.tab=0&gsc.q=obraz%20prostej%20w&gsc.page=1

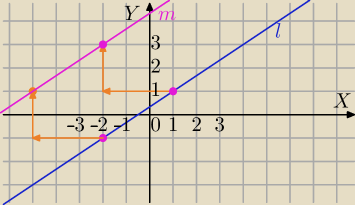
Mila: a) translacja . Obrazem prostej jest prosta równoległa do danej prostej 2x−3y+1=0 Wybieram punkt należący do prostej l, x=1 to 2−3y+1=0⇔y=1 P=(1,1)→T_[−3,2]→P'=(1−3,1+2)=(−2,3) równanie prostej m równoległej do l: m: 2x−3y+D =0 i P'∊m⇔2*(−2)−3*3+D=0⇔−4−9+D=0 D=13 m: 2x−3y+13=0 równanie prostej po translacji ================================ II sposób 3y=2x+1

	2		1
f(x)=		x+		funkcja liniowa
	3		3

Wzór po translacji o wektor [−3,2]: g(x)=f(x+3)+2⇔

	2		1
g(x)=		*(x+3)+		+2
	3		3

	2		1
g(x)=		x+2+2
	3		3

	2		1
g(x)=		x+4
	3		3

	2		13
y=		x+		/*3
	3		3

3y=2x+13⇔2x−3y+13=0 =============== III sposób Wzory na współrzędne punktów po translacji o wektor [−3,2] x'=x−3 y'=y+2 ⇔x=x'+3 i y=y'−2 podstawiamy do równania 2x−3y+1=0 2(x'+3)−3(y'−2)+1=0⇔ 2x'−3y'+13=0 Opuszczamy znaczki(') 2x−3y+13=0 ===============

pigor: ..., czyli IV. ... krótko 2x−3y+1=0 i T_[−3,2] ⇒ 2(x+3)−3(y−2)+1=0 ⇒ ⇒ 2x+6−3y+6+1=0 ⇔ 2x−3y+13=0 . ...

Kacper: Ja lubię sposób V

pigor: ..., a może jeszcze krótko : c) 2x−3y+1=0 i S _(1,−2) ⇒ 2(2*1−x)−3(2*(−2)−y)+1=0 ⇔ ⇔ 2(2−x)−3(−4−y)+1=0 ⇔ 4−2x+12+3y+1= 0 ⇔ 2x−3y−17=0 . ...

pigor: ..., S _{(x= −3)}= T_{[2*(−3), 0]} ◯ S_Oy , czyli złożenie : b) 2x−3y+1 i S_Oy ⇒ 2(−x)−3y+1= 0 ⇔ −2x−3y+1=0 ⇒ ⇒ 2x+3y−1=0 i T_[−6,0] ⇒ 2(x+6)+3y−1=0 ⇔ 2x+3y+11=0 .

123: pigor napisał: " ..., a może jeszcze krótko : c) 2x−3y+1=0 i S (1,−2) ⇒ 2(2*1−x)−3(2*(−2)−y)+1=0 ⇔ ⇔ 2(2−x)−3(−4−y)+1=0 ⇔ 4−2x+12+3y+1= 0 ⇔ 2x−3y−17=0" wg odpowiedzi powinno być: c) 2x−3y+1=0 i S (1,−2) ⇒ 2(x−2*1)−3(y−2*(−2))+1=0 ... 2x−3y=15 P.S. Dzięki za pomoc!