Liczby naturalne .
5-latek:
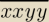
Zadanie oznaczone jako trudne .
Podaj takie dwie cyfry x i y aby liczba xxyy(nad tym jest kreska−nie wiem co to oznacza moze
zapis w systemie dziesiatkowym) byla kwadratem liczby naturalanej
28 sie 01:25
zombi: Zauważmy, że liczbę xxyy, możemy zapisać jako
1000x + 100x + 10y + y, gdzie x∊{1,..,9} a y∊{0,..,9}
Pogrupujmy to w ten sposób
1000x + 10y + 100x + y
10(100x+y) + (100x+y)
11*(100x+y)
Widzimy, że liczba ta dzieli się przez 11
(można to ew. zauważyć z cechy podzielności przez 11, mianowicie (x+y)−(x+y) = 0, co dzieli się
przez 11)
Aby liczba była kwadratem liczba 100x+y musi mieć postać11*k2, z drugiej strony liczba 100x+y
ma postać x0y i znowu z cechy podzielności przez 11 mamy, że x+y − 0 = x+y ma być podzielne
przez 11, czyli x+y=11, szybko znajdujemy takie pary (x,y) tj. (5,6),(7,4),(8,3),(9,2) i
oczywiście (6,5),(4,7),(3,8),(2,9), stąd mamy liczby
100x+y takie:
506, 605, 704, 407, 803, 308, 902, 209. Dzielimy każdą z nich przez 11 i mamy
46, 55, 64, 37, 74, 28, 82, 19
Widzimy, że jedynie liczba 704 spełnia warunek postaci 11*k2. Więc nasza szukana para to x=7
y=4
Co daje odpowiedź, że nasza szukana liczba to 7744.
28 sie 01:41
zombi: Łatwo sprawdzić, że 7744 = (11*8)2
28 sie 01:42
5-latek: Oczywiscie dziekuje .
Ty pewnie byles w klasie matematyczno −fizycznej z tego co widze
Dla mnie na pradwe byloby trudne
28 sie 01:49
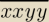 Zadanie oznaczone jako trudne .
Podaj takie dwie cyfry x i y aby liczba xxyy(nad tym jest kreska−nie wiem co to oznacza moze
zapis w systemie dziesiatkowym) byla kwadratem liczby naturalanej
Zadanie oznaczone jako trudne .
Podaj takie dwie cyfry x i y aby liczba xxyy(nad tym jest kreska−nie wiem co to oznacza moze
zapis w systemie dziesiatkowym) byla kwadratem liczby naturalanej