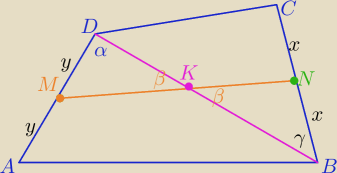
dowód czworokąt wypukły arli28: W czworokącie wypukłym ABCD punkt M jest środkiem boku AD, a punkt N jest środkiem boku BC. Przekątna BD dzieli czworokąt na dwa trójkąty o równych polach oraz przecina odcinek MN w punkcie K. Wykaż, że KM=KN.

arli28: pomocy

Eta: |DB|= d

	1		1
P(ABD)=		*2y*d*sinα , P(BCD)=		*2x*d*sinγ
	2		2

	ysinα
to: ydsinα=xdsinγ ⇒ x=
	sinγ

z tw. sinusów w trójkątach MKD i BKN

	y		|MK|		x		|NK|
		=		i		=
	sinβ		sinα		sinβ		sinγ

	ysinα		xsinγ		ysinα*sinγ		ysinα
|MK|=		i |NK|=		=		=
	sinβ		sinβ		sinγ*sinβ		sinβ

zatem |MK|=NK|

arli28: dzięki