zbadać ciągłość funkcji małgosia: Zbadaj ciągłość poniższej funkcji 1−x² dla x∊(−∞,0) (x−1)² dla x∊<0;2) 4−x dla x∊<2;+∞) Rozwiązałam te zadanie, aczkolwiek potrzebuję Waszego sprawdzenia. x0=0 z lewej strony 1−x²=1−0²=1 z prawej strony (x−1)²=(0−1)²=1 f(0)=(x−1)²=(0−1)²=1 x0=2 z lewej strony (x−1)²=(2−1)²=1 z prawej strony 4−x=4−2=2 f(2)=4−x=4−2=2 Otrzymane wyniki interpretuję tak: W punkcie x0=0 funkcja jest ciągła obustronnie, natomiast w punkcie x0=2 jest ciągła prawostronnie. Czy poprawne jest powyższe rozwiązanie i uzasadnienie? Odpowiedź pod zadaniem brzmi następująco "W punkcie x0=2 ciągła prawostronnie". Dlaczego nie uwzględnia ona punktu x0=2, skoro w moich wynikach wyszło, że spełnia wszystkie warunki? Czy ktoś z Was może mi wytłumaczyć kiedy jest ciągła lewostronnie, a kiedy prawostronnie? Może źle coś robię? Będę bardzo wdzięczna za waszą pomoc

PW: Sama piszesz, że lim(x−1)² = 1 x→2⁻ natomiast f(2) = 2 ≠ 1. Funkcja f nie jest więc ciągła w punkcie 2 (granica lewostronna nie jest równa wartości w x₀=2).. Granica prawostronna w x₀=2 jest równa f(2), co jest określane jako ciągłość prawostronna.

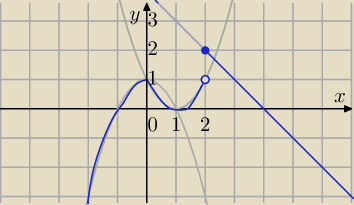Mila: To wykres f(x) (niebieski) w x=2 funkcja nie jest ciągła . (tam wykres "urywa się")