jak zabrać się za tego typu zadanie? Kamil: Podaj liczbę rozwiązań równania: 3^x *(1−x²) =1

Piotr 10: 3^x − x² * 3^x = 1 3^x * x² + 1 − 3^x = 0 Δ= 0 − 4*3^x ( 1 − 3^x ) = − 4*3^x + 4*3^2x = 4*3^2x − 4*3^x = 4 ( 3^2x − 3^x ) Gdy Δ > 0 ( 2 rozwiązania) dla 3^2x − 3^x > 0 3^2x > 3^x x > 0 Gdy Δ=0 ( 1 rozwiązanie) dla 3^2x − 3^x = 0 x=0 Gdy Δ < 0 ( zero rozwiązań) 3^2x − 3^x < 0 x < 0 Jaką masz odpowiedź ?

Kamil: 2 rozwiązania

PW: Piotrze, z teoretycznego punktu widzenia rozwiązanie nie podoba mi się. Nie można liczyć wyróżnika Δ dla funkcji f(x) = 3^xx² + 1 − 3^x, bo to nie jest funkcja kwadratowa. Myślę, że uczeń powinien przekształcić zadane równanie do postaci −x² + 1 = 3^−x, narysować wykresy funkcji występujących po obu stronach i pokazać na rysunku dwa punkty, w których wykresy przecinają się − odcięte tych punktów to rozwiązania.

Piotr 10: PW masz rację, Twój sposób zdecydowanie lepszy

pigor: ..., niestety, ale tu widzę tylko sposób PW , bo drugi (... pierwszy) nie jest żadnym sposobem na to zadanie.

Eta:

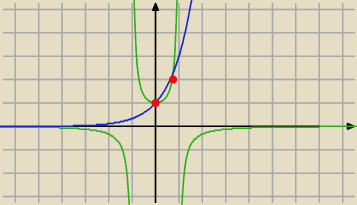
PW: O, i tu widać piękno matematyki. Eta narysowała wykres stosując przekształcenie

	1
3x =		, x∊R\{−1, 1}.
	1−x2

Widać dwa punkty wspólne wykresów, w tym jeden z nich to (0, 1). Ja proponowałem inne przekształcenie: −x² + 1 = 3^−x, dla którego ilustracja będzie zupełnie inna − po lewej stronie parabola, po prawej

	1
(		)x.
	3

W tym wypadku wykresy przetną się znowu w (0, 1), ale drugi punkt wspólny będzie zupełnie inny niż na wykresie z 12:33. I tu konsternacja − czy jeden z tych sposobów jest zły? Nie, oba pokazują te same rozwiązania (x−owe współrzędne punktów, w których wykresy przecinają się).

	1
Ja wolałem parabolę, bo wykres		może nie jest oczywisty dla ucznia.
	1−x2

pigor: ... tak , popieram wykres z parabolą y= −x²+1 i y=3⁻¹ a co do wykresu η−y (... łatwy bez żadnych pomocy graficznych), to brakuje mi na rysunku powyżej "widocznych" asymptot pionowych x=±1. ...