parzystość i nieparzystość funkcji z wart. bezwzględną Zbynek: parzystość i nieparzystość funkcji z wart. bezwzględną f(x) = x + |x| f(−x) = −x + |−x| −f(x) = −x − |x| jak to jest z tą parzystością tych funkcji, bo wykres f(x) i f(−x) wygląda jak byk, że jest symetryczny względem OY, a f(−x) symetryczny względem (0,0) z −f(x). Czy ta funkcja jest parzysta i nieparzysta jednocześnie czy nie jest ani parzysta ani nieparzysta ?

Rafał: A jakie są warunki parzystości i nieparzystości funkcji?

Zbynek: x ∊R ?

Zbynek: f(−x) = f(x) parzystość −f(x) = f(−x) nieparzystość

PW: Coś mącisz proste zagadnienie.

	⎧	2x dla x≥0
f(x) =	⎨
	⎩	0 dla x<0

Widać, że nie jest parzysta ani nieparzysta, bo dla x>0 wartości są dodatnie, a dla x<0 − stale równe 0. Nie może być więc f(−x) = f(x) ani f(−x) = − f(x). Najlepiej narysować.

Zbynek: ok. ale czy ten wniosek ma swoje podstawy w fakcie, że funkcja nie jest różnowartościowa ?

PW: Nie, w fakcie że 0 nie jest równe ani +5, ani −5.

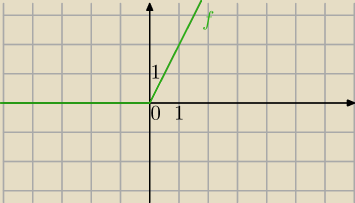
Mila: a) f(x)=x+|x| ani parzysta, ani nieparzysta

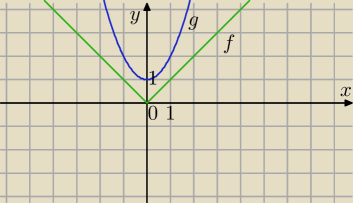
Mila: f(x)=|x| parzysta g(x)=x²+1 parzysta

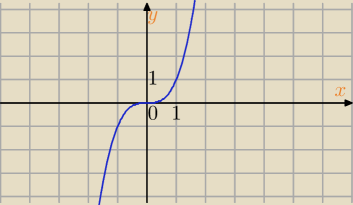
Mila: y=x³ nieparzysta

Zbynek: Dzięki za te przykłady, takie zobrazowanie zawsze bardziej zapada w pamięć

Zbynek: to pytanie do Mila i do reszty użytkowników także: czy istnieje funkcja odwrotna do funkcji: f(x) = −x² gdy x∊(−∞, 0) ?

Zbynek: ok. jest −√x, temat zamknięty

Mila: Tak, bo jest w tym przedziale różnowartościowa.

Mila: Masz błąd. Narysuj , wykres ma być symetryczny względem prostej y=x do tej części paraboli która odpowiada ujemnym argumentom.