trojkąt w okręgu arko: Prosze o rozwiązanie tego zadania http://zalacznik.wp.pl/d685/image003.jpg?p=4&t=IMAGE&st=JPEG&ct=QkFTRTY0&wid=1676&POD=1&type=&zalf=Nowe&tsn=140897715685138895&sid=9536ad55b4163d2fa3657c76231bfcf7

jakubs: #06 Załącznik niedostępny. Prawdopodobnie to żądanie nie pochodzi z poprawnie zalogowanego konta pocztowego.

arko: chodzi o to zadanie http://postimg.org/image/e570k22lf/

Janek191: C. 16 π

Janek191: I CB I = 8√2 , więc I AB I = I CB I*√2 = 16 r = 16 : 2 = 8 L = 2π r = 2π*8 = 16 π

Mila: arko, kąt wpisany oparty na średnicy jest kątem prostym, masz tam Δprostokątny równoramienny. ( połowa kwadratu) Możesz obliczyć średnicę ze wzoru, jak pokazał Janek, albo z tw. Pitagorasa. Zrób tak, bo zauważyłam, że masz z tym problem, a to należy na maturę umieć.

arko: No właśnie tylko jak w AB wyszło mu to 16? zapewne chodzi o jakieś własności trojkąta równoramiennego czyli o to http://static3.opracowania.pl/images/188737/tr%C3%B3jk%C4%85ty_o_k%C4%85tach_90_45_45_stopni_oraz_90_60_30_stopni_01.gif wiem ze w takim trójkącie przeciwprostokątny bo ma miare a pierwiastek z2 ale w tym zadaniu jest jakoś inaczej więc nie wiem jak to zrobić

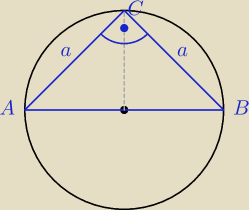
Mila: 1) obliczamy AB z tw. Pitagorasa |CB|=8√2=a AB jest przeciwprostokątną. |AB|²=a²+a² |AB|²=(8√2)²+(8√2)² |AB|²=64*2+64*2 |AB|²=128+128=256 |AB|=√256 |AB|=16 R=8 L=2π*R długość okręgu L=2π*8=16π 2) ze wzoru na przekątną kwadratu d=a√2 |AB|=d=8√2*√2=8*2=16 Dalej tak samo.