wyznacz zbiór wartości
Zbynek: | | 1 | |
wyznacz zbiór wartości f(x) = |
| |
| | 1 + sinx | |
1 + sinx ≠ 0
sinx ≠ −1
| | 3 | |
Df = {x∊R: x ≠ |
| π + 2kπ, k∊Z} |
| | 2 | |
co dalej ? wyznaczyć x ?
y(1 + sinx) = 1
y + ysinx = 1
ysinx = 1 − y
ja tutaj wyznaczyć zbiór wartości funkcji ?
25 sie 16:39
zombi: −1 ≤ sinx ≤ 1
25 sie 16:40
Zbynek: nie, sinx ≠ −1
poza tym należy wyznaczyć zbiór wartości dla f(x) a nie dla sinx
25 sie 16:46
Mila:
| | π | |
Dla x= |
| +2kπ w mianowniku masz największą wartość równą 2.⇔ |
| | 2 | |
| | 1 | |
ymin= |
| − wartość najmniejsza funkcji f(x) |
| | 2 | |
dla x zmierzającego do (−1) z lewej strony w mianowniku otrzymasz bardzo małą liczbę dodatnią
(0
+)
wtedy y dąży do nieskończoności
25 sie 17:11
Janek191:
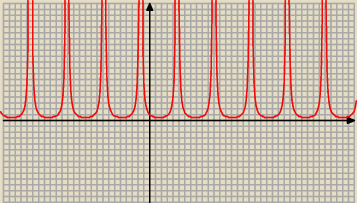
25 sie 17:19
Zbynek: Dzięki Mila i dzięki Janek

25 sie 17:28
Mila:

25 sie 17:29
pigor: ... , a więc ładnie doszedłeś do tego:
sinx = 1−yy =
1y−1 i sinx ≠ −1, no to dalej ma to sens ⇔
⇔ −1<
1y−1 ≤1 /+1 ⇒ 0<
1y ≤2 /*y
2 ⇒ 0< y ≤ 2y
2 ⇔
⇔ y>0 i 2y
2 ≥y /:2y>0 ⇔
y ≥ 12 ⇔
y∊ [12 ;+∞) . ..

25 sie 17:43
Zbynek: właśnie tego brakowało do formalnego zamknięcia zadanie, dzięki za to pigor
25 sie 18:07
Mila:

dla
pigora
26 sie 00:06
pigor: ..., o! dzięki ; miło to dostać od Pani Profesor ;
a ponieważ wpadłem tylko na chwilę, mówię dobranoc. ...

26 sie 00:52




 dla pigora
dla pigora
