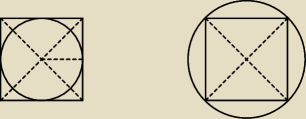 Oblicz stosunek objętości kuli wpisanej w walec do objętości kuli opisanej na tym walcu. Jeżeli
chcemy wpisać/opisać na tym walcu kulę to przekrój osiowy musi być kwadratem.
Vkw−Objętość kuli wpisanej
Vko−Objętość kuli opisanej
Oblicz stosunek objętości kuli wpisanej w walec do objętości kuli opisanej na tym walcu. Jeżeli
chcemy wpisać/opisać na tym walcu kulę to przekrój osiowy musi być kwadratem.
Vkw−Objętość kuli wpisanej
Vko−Objętość kuli opisanej
|
| ||||||||||||||||||||||||
Vkw3/Vko3= | = | = | |||||||||||||||||||||||
|
|
| Vkw | Rw3 | Rw | |||
= | = 3√ | =.... | |||
| Vko | Ro3 | Ro |
| a | a√2 | |||
gdzie Rw= | , Ro= | |||
| 2 | 2 |
| √2 | ||
A w odpowiedzi mam podane | ||
| 4 |
| 1 | ||
Pomyłka 3√√ | ||
| 2 |
 źle mi się wpisało
źle mi się wpisało
| Vkw | Rw | ||
= ( | )3 =...... | ||
| Vko | Ro |
| √2 | 2√2 | |||
...= ( | )3= | = ....... | ||
| 2 | 8 |
| 1 | ||
A jak zrobić z | poprawny wynik ?  | |
| 2√2 |
| 1 | √2 | √2 | |||
* | = | ||||
| 2√2 | √2 | 4 |




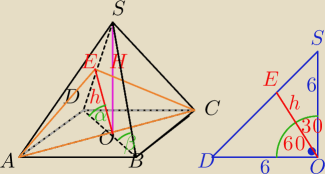 α=60o,β=45o
H=6
ΔSOB− Δprostokątny równoramienny
H=|SO|=|OB|=6
|OD|=6
α=60o,β=45o
H=6
ΔSOB− Δprostokątny równoramienny
H=|SO|=|OB|=6
|OD|=6
| 1 | 1 | |||
PΔACE= | *|AC|*h= | *12*h | ||
| 2 | 2 |
| 1 | ||
PΔDOS= | *6*6=18 | |
| 2 |
| 1 | 1 | |||
PΔDOS= | *6*h*sin60+ | *6*h*sin300⇔ | ||
| 2 | 2 |
| √3 | 1 | |||
3*h* | +3h* | =18 /:3 | ||
| 2 | 2 |
| √3 | 1 | |||
h* | +h* | =6 /*2 | ||
| 2 | 2 |
| 1 | ||
PΔACE= | *12*h=6*6*(√3−1) | |
| 2 |

