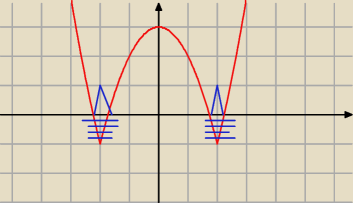
zbiór Blue: Równanie ||x²−4|−1| = p ma dwa rozwiązania dla : A. p∊{−1}U<3,∞) B. p∊{−1}U(3,∞) C. p∊<−1, 3> D. p∊(3,∞) Czy to jest tak, że te opcje, w których p jest mniejsze od zera powinny by od razu odrzucone Bo przecież całe wyrażenie jest pod wartością bezwzględną...

bezendu: p∊(3,∞) Całe wyrażenie jest pod wartością bez ? Skoro całe wyrażenie jest w module, to wykres jest nad osią OX.. Poczytaj teorię ...

Piotr 10: Dla p < 0 będzie 0 rozwiązań,np: I I x² − 4I − 1 I = −3 Nas interesuje dla jakich p równanie ma dwa rozwiązania, czyli dla dodatnich p

Blue: No właśnie więc zaznaczyłam odp. D , no bo wiadomo, że p nie może być mniejsze od zera, ale w odpowiedziach jest inaczej ! :C tam jest odp. B , a ja nie wiem dlaczego:<

Blue: Czyli mam rozumieć, że znowu błąd jest w tym i jednak odp. D jest poprawna?

Marek: B by było tylko jeśli by nie było drugiej wartości bezwzględnej. Wygląda na błąd w zbiorze.

Blue: Ten zbiór jest do kitu:c Ale przynajmniej mam pewność , że się nie myliłam, dzięki

bezendu: To trzeba było kupić zbiór A.Kiełbasy..