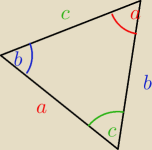
trygonometria, twierdzenie sinusów Dejf: Wykaż że jeśli α,β są miarami dwóch kątów trójkąta, a R jest promieniem okręgu opisanego na tym trójkącie, to obwód trojkąta jest rowny 2R[sinα+sinβ+sin(α+β)]. Narazie mam to:

a
	=2R ⇔ a=sinα*2R , dalej analogicznie:
sinα

b=sinβ*2R c=sinγ*2R zatem: a+b+c=sinα*2R+sinβ*2R+sinγ*2R = 2R(sinα+sinβ+sinγ) tylko co dalej jak tylko co dalej zrobic zeby sinγ byl rowny sin(α+β) − gdzie jest haczyk

Piotr 10: Trzeci kąt δ= 180⁰ − ( α+β)

Dejf: a nie 180−α+β? − tak probowalem i niewychodzi , czrmu ten nawias

Dejf: to jakis wzor redukcyjny?

Piotr 10: Suma kątów wewnętrznych w trójkącie wynosi 180⁰ Jeżeli mamy dany kąt alfa i kąt beta to kąt gamma wynosi γ = 180⁰ − α − β = 180⁰ − ( α+β) Wzory redukcyjne: sin ( 180⁰ − δ ) = sinδ − ogólny przypadek

Dejf: dziena