trudne zadania - matura rozszerzona Patryk95: >>STEREOMETRIA<< Zad. 1 W czworoscianie o podstawie ABC i wierzcholku D poprowadzono plaszczynzneprzechodzaca przez srodki krawedzi AB, BD, CD. Plaszczyzna ta dzieli czworoscian na dwie bryly. Wyznacz stosunek objetosci tych bryl. [odp. V₁ = V₂] Zad.2 Podstawa ostroslupa jest kwadrat o boku dlugosci a. Dwie przylegle sciany boczne ostroslupa sa prostopadle do plaszczyzny podstawy, a kazda z pozostalych scian tworzy z plaszczyzna podstawy kat α. Oblicz pole powierzchni bocznej ostroslupa. [odp. Pb = a²(sinα+1)/cosα] Zad.3 Podstawa ostroslupa jest trojkat rownoboczny o boku dlugoscci a. Jedna z krawedzi bocznych o dlugosci b tworzy z przylegajacymi krawedziami podstawy kat a. Wyznacz objetosc ostroslupa. [odp. V=a²b√3−4cos²α/12] Z gory dziekuje za pomoc bo prawdopodobnie jutro odczytam i/lub sprobuje rozwiazac.

pb: W zad. 1. najlepiej tak: zakladasz ze caly ostroslup ma powiedzy objetosc V₀, i liczysz "nowa" objetosc, o tej samej podstawie. Wystarczy "nowa" wysokosc odszukac, i stosunek wyjdzie V_x / V₀ = V_x. Wiec wysokosc musi wyjsc 1/2 calego ostrosupa.

pb: stosunek: V_x / V₀ − V_x

Godzio: 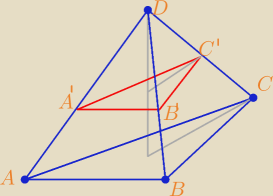Zad. 1 Zacznijmy od faktu o odcinku łączącym środki ramion trójkąta, z niego mamy

	1
|A'B'| =		|AB| (itd. z innymi bokami)
	2

Trójkąty ABC i A'B'C' są podobne w skali 2

PABC
	= 4
PA'B'C'

	1
H' =		H
	2

	1		1
VABCD =		PABCH =		* 4PA'B'C' * 2H' = 8 * VA'B'C'D
	3		3

VABCC'B'A'		VABCD − VA'B'C'D
	=		=
VA'B'C'D		VA'B'C'D

	8 * VA'B'C'D − VA'B'C'D
=		= 7
	VA'B'C'D

Eta: Hej Godzio ... jaki piękny rys.

Bogdan: W zadaniu 1 jest mowa o środku krawędzi AB, a nie AD (prawdopodobnie pomyłka Patryka)

Eta:

V1
	= k3 , k −−− skala podobieństwa
V2

Bogdan: A przy okazi − zawsze ostrosłup lub stożek przecięty płaszczyzną równoległą do podstawy w połowie wysokości bryły dzieli ją na dwie bryły o stosunku 7 : 1, co wynika z własności figur podobnych o skali k. Jeśli k = 2, to stosunek objętości powstałych brył jest rowny k3 = 8.

Bogdan:

KUZDE: Tak, tylko ze tutaj nie chodzi o plaszczyzne rownolegla do podstawy

KUZDE: Zaraz wstawie rozwiazanie

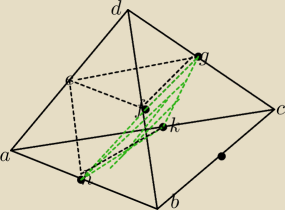
KUZDE: Nie umiem ladnego rysuknu zrobic ale juz nie bede tracil czasu Ale jak wczesniej podane osroslup (caly) ma objetosc V.

	V
Ostroslup o krawedziach mniejszych o polowe, bedzie objetosci
	8

A jedna z powstlych czesci (ADGFH),(h− srodek AB ) slkada sie z 4 takich ostrosłupów. dokadniej ( EFGD),(AEHK),(KGFH),(EFHK)

KUZDE: powstalych czesci (ADGKH)*

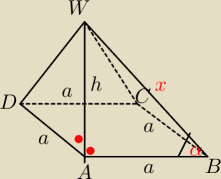
Janek191: Mamy

h
	= tg α ⇒ h = a tg α
a

x² = a² + h² = a² + a² tg² α = a² *( 1 + tg² α ) x = a p{ 1 + tg² α ) PΔ_ABW = 0,5 a*h = 0,5 a*a tg α = 0,5 a² tg²α PΔ_BCW = 0,5a *x = 0,5 a* a √1 + tg² α = 0,5 a² √1 + tg² α Pole powierzchni bocznej ostrosłupa P_b = 2 PΔ_ABW + 2 PΔ_BCW = a² tg² α + a² √1 + tg² α = = a² *( tg α + √ 1 + tg² α) ============================ lub

	sin α		cos2 α + sin2 α
Pb = a2 *(		+ √		) =
	cos α		cos2 α

	sin α		1		sin α + 1
= a2*(		+		) = a2 *
	cos α		cos α		cos α

Patryk95: Dzieuje za wszystkie odpowiedzi. Zadanie 3. chcialem tak zrobic. V=a²√3/12 * H H = b² − R², gdzie R − promien okregu opisanego na podstawie, ale wyniki sie nie pokrywaja.