PW: Najpierw przestrzeń zdarzeń elementarnych Ω. Losujemy dwa razy po jednej kuli bez zwracania. W
treści zadania nie ma mowy o ustawianiu wylosowanych kul w kolejności losowania, po prostu
pytają czy kule są jednakowego koloru. Wobec tego możemy uznać, że takie losowanie jest
równoważne wylosowaniu dwóch kul jednocześnie, czyli wyodrębnieniu 2−elementowego podzbioru ze
zbioru 22−elementowego. Tak więc Ω jest zbiorem wszystkich 2−elementowych kombinacji
(podzbiorów) ze zbioru 22−elementowego.
Niech N oznacza zdarzenie "obie wylosowane kule są niebieskie", a C − "obie wylosowane kule są
czerwone". Zdarzenie A − "wylosowano obie kule tych samych kolorów" jest sumą:
A = N∪C,
a ponieważ N i C są rozłączne
(2) P(A) = P(N) + P(C).
| | | | | |
(3) |N| = | = 11•6, |C| = | = 9•5. |
| | | |
Z treści zadania wynika, że wszystkie zdarzenia elementarne są jednakowo prawdopodobne,
stosujemy więc twierdzenie zwane klasyczną defnicją prawdopodobieństwa:
| | |N| | | |C| | |
(4) P(N) = |
| , P(C) = |
| . |
| | |Ω| | | |Ω| | |
Podstawienie (1) i (3) do (4) i do (2) daje rozwiązanie.
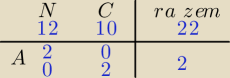 albo bez drzewka (metodę drzewka ktoś kiedyś nazwał tu krzakoterapią}
albo bez drzewka (metodę drzewka ktoś kiedyś nazwał tu krzakoterapią}
 Skorzystaj z twierdzenia o prawdopodobieństwie całkowitym
Skorzystaj z twierdzenia o prawdopodobieństwie całkowitym 