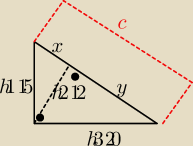
rowania kwadratowe Dejf: W trójkącie prostokatnym wysokości mają długość 12 15 i 20. Jaka długość mają odcinki, na które spodek wysokości poprowadzonej z wierzchołka kąta prostego, podzielil przeciwprostokatna? Mam nadzieje ze dobrze oznaczylem boki − wysokość poprowadzona z wierzcholka kata prostego jest zawsze najmniejsza. 1.sposób c=√15²+20² c=25 25=x+y y=√400−144 y=16 wiec po podstawieniu do poprzedniego rowniania x = 9 Lecz proszę o pomoc przy drugim sposobie na to zadanko: W trojkacie prostokatnym wysokość poprowadzona z wierzcholka kata prostego rowna sie pierwiastkowi z iloczynu dlugosci odcinkow ktore tworzy na przeciwprostokatnej wiec taka mysl przyszla mi do glowy ze mozna sie pobawic w rownianie kwadratowe zatem ulkad rownan: 12=√xy 25=x+y

	144
144=xy ⇒		= x no i podstawiamy i mamy ronianie kwadratowe tylko mi wychodza dwa
	y

rozwiazania dodatnie 9 i 16 a tak niemoze byc.... − pomoze ktoś PS Δ = 652 −574=49 Małe równanko: y²−25+144=0 y1 wychodzi mi 9 a y2 16

Bogdan: Przyprostokątne w trójkącie prostokątnym są wysokościami tego trójkata, ortocentrum znajduje się w wierzchołku kąta prostego.

Kacper: Dzisiaj jestem ślepy Idę odpocząć

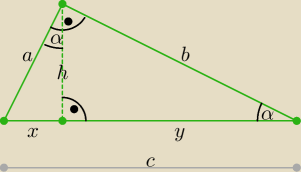Bogdan: Zachodzą tu związki:

1		1		a*b
	*c*h =		*a*b ⇒ h =		,
2		2		c

x		h
	=		⇒ h = √x * y,
h		y

x		h		a*h		y		h		b*h
	=		⇒ x =		,		=		⇒ y =
a		b		b		b		a		a

x		a		a2		y		b		b2
	=		⇒ x =		,		=		⇒ y =
a		c		c		b		c		c

Dejf: no ale nikt mi jeszcze nie pomogl, czy ten pomysl z ukladem rownan byl zly?

Eta: Dwa razy twierdzenie Pitagorasa i po bólu x=√400−144=....... y=√225−144=.......

Eta: Nie zauważyłam,że na Twoim rys. y=√400−144=..... x=√225−144=...

Dejf: no tak ..... ale czemu z tym ukaldem rownan nie wychodzi − przecierz odcinek niemoze miec jednoczesnie 9 i 16cm Zaraz sie wkurze o podre ksizke od maty

Mila: Napisz założenie. x<y