oblicz przedzialy monotonicznosci i ekstrema lokalne
lokowanie: f(x)=(ex)/x2
24 sie 17:24
razor: pochodna wyliczona?
24 sie 17:26
lokowanie: (ex(x−2))/x3
24 sie 17:27
razor: | | ex(x−2) | |
dobrze, to teraz do rozwiązania równanie |
| = 0 i badamy znak funkcji w okolicy |
| | x3 | |
miejsca zerowego
24 sie 17:31
razor: znak pochodnej*
24 sie 17:32
Janek191:
OK
x ≠ 0
f ' (x) = 0 ⇔ x = 2
24 sie 17:33
lokowanie: f(x)=0 dla x=2
f(x)>0 dla (2;
∞)
f(x)<0 dla (−
∞;0)u(0;2)
24 sie 17:35
Janek191:
Powinno być f ' (x)
24 sie 17:36
lokowanie: no wiem i co teraz dalej tu sie gubie
24 sie 17:38
Janek191:
Wniosek : minimum lokalne dla x = 2
Dla x < 0 jest f '(x) > 0
24 sie 17:39
Janek191:
Funkcja rośnie w ( − ∞ ; 0 ) , ( 2 ; + ∞)
Funkcja maleje w ( 0 ; 2)
x = 0 − asymptota pionowa
24 sie 17:41
Janek191:
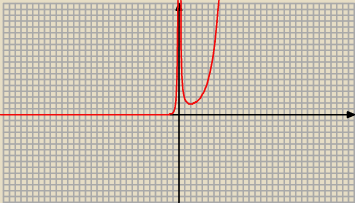
24 sie 17:42
lokowanie: Funkcja rośnie w ( − ∞ ; 0 ) ?
24 sie 17:43
Janek191:
Nie widać na wykresie ?
24 sie 17:44
Janek191:
Dla x < 0 jest ex > 0 , x − 2 < 0 i x3 < 0 czyli f ' (x) > 0
24 sie 17:47