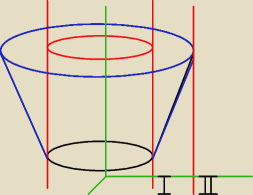
Oblicz objętość bryły ograniczonej powierzchniami. kompan: Czołem Oto powierzchnie : 3x²+3y²≤z² x²+y²+z²≤25 x²+y²+z²≤9 Po naszkicowaniu funkcji wyjdzie bryła przypominająca korek. Korek od dołu i góry jest ograniczony wierzchołkami SFER, a nie płaskimi powierzchniami jak jest na rysunku. Innymi słowy jest zaokrąglony. Nie wiem jak zabrać się za całkę potrójną więc zacząłem liczyć objętość z sumy całek podwójnych. Podzieliłem figurę na 2. Pierwsza to walec ograniczony sferami, drugi to pierścień ograniczony od dołu stożkiem, od góry sferą. Na rysunku liczby I i II to odpowidnio 1,5 i 2,5 − promień walca oraz promień zewnętrzny pierścienia, wewnętrzny to 1,5. Problem pojawia się już w pierwszej całce (walec), wynik mam ujemny. Górna funkcja to większa sfera, dolna funkcja to mniejsza sfera. Po przejściu na współrzędne biegunowe. 0≤φ≤2π wewnętrzna całka : 0≤r≤1.5 ∬( r√25−r²−r√9−r² ) dr dφ = ∬ (¹₃(9−r²)^3₂−¹₃(25−r²)^3₂ dφ w tym etapie za 'r' podstawić 1,5 i przemnożyć przez 2π (całka oznaczona) tu jest ujemny wynik. Druga całka to pierścień. 0≤φ≤2π 1.5≤r≤2.5 √3x²+3y² ≤ z ≤√25−x²−y² √3r²≤ z ≤√25−r² <−− w. biegunowe ∬(√25−r²−√3r²)r dr dφ gdzie wynik wychodzi ~25*2π nieco zawyżony Czy źle definiuje całki ? Wiecie jak ten problem opisać w jednej całce ? pozdrawiam

kompan: Uwaga, na początku zadania wkradł się błąd Ostatnia sfera to : x2+y2+z2 ≥ 9 9 ma być mniejsze od...