uklad rownan Gloksa: Hello. Czy ktos moglby mi rozwiazac krok po kroku ten uklad rownan? Nie wiem jak wstawic klamre, ale to ma byc zamkniete w klamrze x*y = 48 x²+y² = 100

Piotr 10: x*y = 48 * 2 2xy = 96 (x+y)² = 100+96= 196 Ix+yI = 14 x+y = 14 v x+y = − 14 Wstawiasz do I równania i masz równanie z jedną niewiadomą

5-latek: A w jakich liczbach ma to byc rozwiazane bo jesli w liczbach naturalnych to x*y i x i y nalezy do N 6*8=48 6²+8²=100 wiec x=6 i y=8 lub x=8 i y=6

Kacper: można np tak:

	48
y=
	x

	48
x2+(		)2=100
	x

	482
x2+		=100 |*x2
	x2

x⁴+48²−100x²=0 x²=t, t≥0 i teraz jak zwykłe kwadratowe

5-latek: Czesc Piotr

Kacper: Piotrek pierwszy pomysł był jak identyczny jak twój cześć 5−latek

Piotr 10: Witam . Po co bawić się w równanie dwukwadratowe

5-latek: Witaj [N[Kacper] Wiem ze masz jeszce tydzien wolnego ale czy bedziesz wieczorem na forum ,gdyz dopiero dobrze funkcjonuje wieczorem

Kacper: O ile będzie taka możliwość to zawsze Zresztą muszę kontrolować czy moi uczniowie będą pytać o rozwiązania zadań

Piotr 10: A kiedy jest poprawka matury , którego sierpnia ?

PW: Pomysł 5−latka bardzo mi się podoba. Nikt nam nie broni spróbować, czy nie ma rozwiazań w liczbach naturalnych. Znaleźliśmy dwa, bez żadnych skomplikowanych działań. Teraz jeszcze tylko sprawdzić, czy nie ma innych. Toż to hiperbola i okrąg − rysujemy ilustrację, która przypomina, że istnieją jeszcze rozwiązania symetryczne (ujemne) i koniec.

5-latek: Piotrek slyszalem ze 26 sierpnia jest poprawka

Kacper: W ten wtorek wszyscy piszą poprawkę

Piotr 10: Ok.Thx Trzeba wiedzieć, bo jeszcze ktoś na forum napisze zadania a je rozwiąże

5-latek: Dzien dobry PW

Gloksa: Dzieki! Zadanie potrzebowalam dla kolegi (mieszkam w Szwajcarii). Kolega: "Przeciez nigdy ci tak szybko nie odpisza, sa wakacje". Ja: "Odpisza. Dzieki nim zdalam mature. Mam doswiadczenie z tym forum". Po Waszej szybkiej i konkretnej odpowiedzi, kolega stwierdzil, ze dla tego forum zacznie sie uczyc polskiego. Pozdrawiam.

Michał : Równie dobrze można pomnożyć pierwsze równanie przez −2 i zrobić resztę zadania tak jak Piotr 10( korzystamy ze wzoru x²−2xy+y²=(x−y)²)

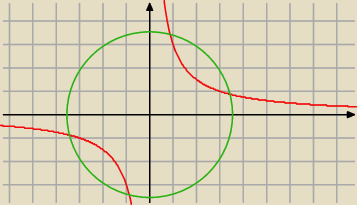
Trivial: PW, jeszcze lepiej zauważyć, że możliwych rozwiązań jest co najwyżej 4 (patrz rysunek) oraz że równania są symetryczne w taki sposób, że jeżeli (x,y) jest rozwiązaniem, to rozwiązaniami są też (−x,−y), (y,x), (−y,−x). Potem odgadnąć rozwiązanie (6,8) i wypisać resztę.