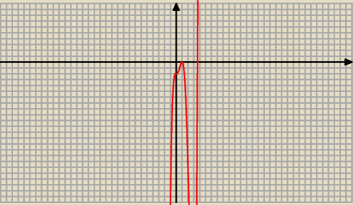
Ekstremum lokalne i monotoniczność Zocha: Proszę pomóżcie mi bo albo godzina nie ta, albo coś mi się maga pokręciło. Mam zadanie z e−trapeza policzyć ekstremum lokalne i monotoniczność. dla funkcji f(x) = 2x⁵−10x⁴+10x³−2 Mi tu wychodzą 3 miejsca zerowe, 0, 1 , 3. A w e−trapezie jest tylko x=1 i x=3.

Cyber Marian: http://www.wolframalpha.com/input/?i=2x%5E5%E2%88%9210x%5E4%2B10x%5E3%E2%88%922%3D0

jakubs: f(0)=0−0+0−2 f(0)=−2

Zocha: Wynik pochodnej 10x⁴−40x³₃0x² Prze nawias wyciągam 10x² i mam 10x²(x²−4x+3)

jakubs: Pochodna dobrze.

Janek191: f' (x) = 10 x⁴ − 40 x³ + 30 x² = 10 x² *( x² − 4 x + 3) = 10 x² *( x − 1)*( x − 3) f ' ( x) = 0 ⇔ x = 0 lub x = 1 lub x = 3 Obliczam II pochodną : f '' (x) = 40 x³ − 120 x² + 60 x = 20 x*( 2 x² − 6 x + 3 ) Obliczam : f ''( 0) = 0 oraz f '' ( x ) < 0 dla x ∊ ( 0 − δ ; 0 ) f '' ( x) > 0 dla x ∊ ) 0 ; 0 + δ ) , gdzie δ > 0 ( np. δ = 0, 1 ) zatem funkcja f ma w punkcie x = 0 punkt przegięcia. −−−− f '' ( 1) = 40*1 − 120*1 + 60*1 = − 20 < 0 zatem f ma w punkcie x = 1 maksimum lokalne −−−− f '' ( 3) = 40*27 − 120*9 + 60*3 = 1 080 − 1 080 + 180 = 180 > 0 zatem f ma w punkcie x = 3 minimum lokalne.