wektory
anaaa: Narysuj czworokąt ABCD , jeśli wiesz,że jego kolejne wierzchołki są wyznaczone przez wektory
AB= [6,7] , BC= [−5,7] , CD=[−4,−7] , DA=[3,−7] . Oblicz pole tego wielokąta.
23 sie 16:57
PW: Skąd Ty bierzesz takie dziwne zadania? Znowu − jak w poprzednim zadaniu z trójkątem − problem
leży w takim sformułowaniu zadania przez autora, żeby uczeń nie rozumiał o co idzie.
Zdajesz sobie sprawę, że wektor [6, 7] jest to twór, którego tak naprawdę nie można narysować
na płaszczyźnie? Czego od Ciebie chce autor, gdy mówi, że wektor AB = [6, 7] wyznacza
wierzchołki czworokąta?
23 sie 17:19
anaaa: No właśnie nie wiem
23 sie 17:37
PW: Bierzesz dowolny punkt płaszczyzny i nazywasz go A. W punkcie A zaczepiasz wektor, który
ma współrzędne takie jak wektor [6, 7]. W ten sposób otrzymasz punkt B − koniec tego wektora.
W punkcie B zaczepiasz wektor, który ma współrzędne takie jak wektor [−5, 7] ... i tak dalej.
Złośliwość autora polega na tym, że wierzchołki szukanego czworokąta nazwał tak jak wektory:
zapis AB = [6, 7] jest kretyński, powinno być u→ = [6, 7].
Jeżeli uda się w ten sposób jak napisałem (wielokąt "zamknie się", to znaczy koniec ostatniego
wektora pokryje się z początkiem pierwszego), to pół biedy. Próbuj, z rysowaniem w układzie
współrzędnych. Wystartuj np. od A = (1, 1) − wolno tak zrobić, zadanie ma nieskończenie wiele
rozwiązań.
23 sie 17:50
Mila:
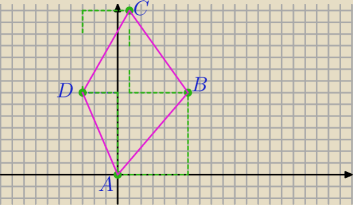
A=(0,0)
23 sie 17:59
anaaa: Dzięki

23 sie 18:00
PW: Mila, miło Cię "widzieć". Znowu wychodzę na takiego, co się znęca nad młodzieżą zamiast
dać im gotowe rozwiązanie

A swoją drogą dziwny ten autor, nie chciałem już pisać o różnicy między wektorem swobodnym a
jego reprezentantem.
anaaa, wierz mi (spróbuj lepiej sama) − zaczynając od A = (1, 1) albo A = (π,
√3) też
otrzymasz tak samo dobre rozwiązanie
23 sie 18:16
Mila:
Witaj, PW, masz rację co do treści zadań.
Ana powinna narysować począwszy od innego punktu. Wtedy zrozumie problem.
23 sie 18:23
 A=(0,0)
A=(0,0)

 A swoją drogą dziwny ten autor, nie chciałem już pisać o różnicy między wektorem swobodnym a
jego reprezentantem.
anaaa, wierz mi (spróbuj lepiej sama) − zaczynając od A = (1, 1) albo A = (π, √3) też
otrzymasz tak samo dobre rozwiązanie
A swoją drogą dziwny ten autor, nie chciałem już pisać o różnicy między wektorem swobodnym a
jego reprezentantem.
anaaa, wierz mi (spróbuj lepiej sama) − zaczynając od A = (1, 1) albo A = (π, √3) też
otrzymasz tak samo dobre rozwiązanie