[C[Analiza jest trudna]]
Radek:
Oblicz granicę.
21 sie 21:36
Kacper: a po co wyłączasz to n?

21 sie 21:36
Kacper: | | 1 | | 1 | |
po prostu limn→∞ |
| =[ |
| ]=0  |
| | n+1 | | ∞ | |
21 sie 21:37
Radek:
A czemu nie ? Wyciąganie przed nawias stosuję.
21 sie 21:37
21 sie 21:39
Radek:
2. limn→∞(n2+1)
limn→∞=∞
[∞+1]=∞ ?
21 sie 21:52
jakubs: tak
21 sie 21:53
Radek:
A pierwsze czemu źle ?
21 sie 21:56
Kacper: Nie powiedziałem, że źle

Tylko w ogóle nie potrzebne
21 sie 21:57
jakubs: | | stała | |
Dobrze, tylko niepotrzebnie wyciągałeś przed nawias, bo to jest oczywiste: |
| =0 |
| | ∞ | |
21 sie 21:57
Mila:
Radek, dobrze, ale niepotrzebna fatyga, bo w liczniku masz stałą a w mianowniku
nieskończoność.
21 sie 21:58
Radek:
Będzie Pani jeszcze na forum ?
21 sie 21:59
Mila:
Jestem.
21 sie 22:00
21 sie 22:02
Mila:
Tak.
21 sie 22:05
21 sie 22:07
Mila:

Tak.
21 sie 22:16
21 sie 22:20
jakubs: Dobrze

21 sie 22:22
21 sie 22:26
Mila:
Dobrze.
21 sie 22:33
Radek:
Dziękuję, tę proste już ogarniam potem są o wiele trudniejsze.
21 sie 22:47
Mila:
Powolutku, wszystko się opanuje.
21 sie 23:04
Radek:
| | 1+2+3+...n | |
limn→∞ |
| cosn! |
| | n3+1 | |
Silnia i jeszcze trygonometria to już koszmar.
21 sie 23:11
Mila:
1) oblicz sumę w liczniku
2) Potem zobaczymy do czego dąży ułamek, na razie .
21 sie 23:14
Piotr 10: W liczniku masz sumę skończonego ciągu arytmetycznego.
21 sie 23:15
Piotr 10: odpowiedź to 0 ?
21 sie 23:18
Radek:
pomocniczo policzyłem sumę i mam
21 sie 23:19
Mila:
| | n2+n | |
3) Ułamek |
| →0 (dąży do 0.) |
| | 2n3+2 | |
Jest takie twierdzenie :
jeżeli a
n→0 i b
n to ciąg ograniczony to
(a
n*b
n) →0
Tu właśnie masz taką sytuację, bo |cos(n!)|≤1, czyli ciąg ograniczony.
4)....
21 sie 23:24
Mila:
|cos(n!)|≤1 ⇔ten ciąg jest ograniczony.
4) Jeżeli
a
n→0 i b
n−c. ograniczony to ,
(a
n*b
n)→0
5)....Raduś dokończy z ładnym zapisem.
21 sie 23:27
Radek:
Właśnie ja nie wiem kiedy jest ograniczony i wgl te sprawy. Tego twierdzenia również nie znam.
21 sie 23:27
Mila:
Przecież wiesz jak wygląda wykres cosinusa. Wartości od (−1) do 1.
A tw. Ci podałam. Pisałam, powolutku przyswaja się materiał.
21 sie 23:31
Radek:
ale tam jest cosn!
21 sie 23:32
Mila:
Nie szkodzi. Wykres cosinusa nie wyskoczy do góry ponad 1 ani nie obniży się poniżej (−1).
Poproś wolframa, aby obliczył cos(100000000).
21 sie 23:36
Radek:
Nie znam się na wolframie. Dziękuję jutro do tego wrócę. Dobranoc
21 sie 23:38
Ajtek:
Niech n!=x, to cos(n!)=cos(x) ⇒ Zw cos(x).... ⇒ Zw cos(n!)....

Hej
Mila,
Piotr10, jakubs,
bezendu 
.
21 sie 23:40
Piotr 10: Witam

21 sie 23:41
Mila:

Witam i dobranoc wszystkim, nic już nie myślę.
Radek , poznaj sie na wolframie, pomaga , możesz tam sprawdzać obliczone wyniki.
21 sie 23:45
Radek:
ale tam jest wyraznie cosn! a nie cosn
22 sie 17:03
zombi: ALE TO NIE ZMIENIA OGRANICZENIA COSINUSA
−1 ≤ COS(BYLECZEGO) ≤ 1
22 sie 17:11
Janek191:
Masz − 1 ≤ cos x ≤ 1 , czyli dla x = n !
jest − 1 ≤ coa n ! ≤ 1
22 sie 17:11
Radek:
a jak by było cos(2x+1) albo cos(2x) ?
22 sie 17:17
Mila:
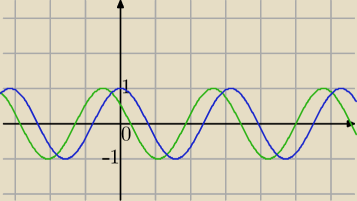 |cos(2x+1)|≤1
|cos(2x+1)|≤1 patrz na wykres.
|cos(2x)|≤1
22 sie 17:24
Radek:
Z trygonometrią miałem duże problemy i nie do końca chyba jeszcze rozumiem.
22 sie 17:26
Mila:
Wartości "wahają się " od (−1) do 1 dla argumentów z zakresu (−∞) do (∞).
22 sie 17:29
Radek:
A jak by tam był tgn! ?
22 sie 17:43
22 sie 18:39
Mila:
Z tym byłby problem, na razie tam go nie ma. Z tangensem inaczej są dobierane wzory i też da
| | π | |
się obliczyc. Tangens nie jest określony w x= |
| +kπ. |
| | 2 | |
22 sie 18:41
Radek:
zdecydowanie wole algebrę.
22 sie 18:46
Mila:
Nie uciekniesz od tego, musisz to opanować.
Rysuj wykresy funkcji trygonometrycznych i badaj własności.
22 sie 19:08
Radek:
Wiem, że nie ucieknę. (niestety)
22 sie 19:58
Radek:
Rysuje i nic to jakoś nie dało ?
22 sie 22:42
Radek: i skąd mam wiedzieć kiedy jest ograniczony ?
23 sie 17:16
Mila:
Ograniczony to oznacza, że wartości funkcji należą do skończonego zbioru liczb albo do
przedziału
[a,b], albo (a,b), gdzie a i b to konkretne liczby
an=(−1)n
zbiór wartości {−1,1}
sin(nπ) , sin(nx) jakie mają zbiory wartości?
23 sie 17:21
Radek:
sin zw<−1,1> nie wiem jak sin(nπ) i sin(nx)
23 sie 17:26
Mila:
sin(nπ) licz po kolei
sin(0*π),sin(1π), .. itd
|sin(nx)|≤1
zw=<−1,1>
23 sie 17:48
Radek:
A może Pani pokazać jak mam to liczyć ?
23 sie 18:05
Mila:
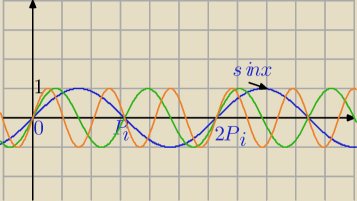
1) sin0=0
sin(π)=0
sin(2π)=0 przecież znasz te podstawowe wartości.
2) rysowanie funkcji sin(nx) przecież też miałeś w szkole.
a) y=sin(1*x) patrz wykres.
b) [z[y=sin(2x)] zagęszczenie wykresu
c)
y=sin(3x)
Jak widzisz wartości są w przedziale <−1,1>
23 sie 18:20
Radek:
No tak miałem w szkole.
23 sie 18:37
Mila:
Rozumiesz już ?
23 sie 19:00
Radek:
Chyba tak. czyli sin zawsze będzie ograniczony ? cos również. ?
23 sie 19:18
Mila:
Tak.
23 sie 19:23
Radek:
czyli nawet jak będzie sin(2x+coś tam) to on jest ograniczony. ?
23 sie 19:25
Kacper: 
23 sie 19:30
23 sie 19:38
Mila:
Trening i czytanie wzorcowych rozwiązań.
23 sie 20:48
Eta:
@
Radek trening .... czyni mistrza

Powodzenia na "treningach"

23 sie 20:54
Radek:
Ale to mnie przeraża. bo nie wiem co i jak. A bez sensu jest wstawiać każde zadanie na forum.
Może politechnika to nie był dobry wybór.
23 sie 20:56
Radek:
limn→∞log(logn) i znowu jestem debilem bo nie wiem ?
23 sie 21:25
Mila:
log(n)→∞ dla n→∞, to ....
23 sie 21:28
Radek:
Nie wiem. mówiłem, że nic z tego nie rozumiem

23 sie 21:29
Mila:
Log(x) przy podstawie (10) a więc większej od 1 jest funkcją rosnącą , znasz wykres.
Log(n) dąży do nieskończoności, to log(log(n)) też dąży do nieskończoności.
23 sie 21:34
jakubs: Radek ja też mam sporo problemów z analizą, ale powolutku, powolutku...

23 sie 21:37
Radek:
Dziękuję Pani.. Ale to chyba trzeba być geniuszem na to. żeby to wszystko skojarzyć.
23 sie 21:42
Mila:
Nie jestem geniuszem i kojarzę, Ty też potrafisz.Powolutku.
23 sie 22:18
Radek:
Dla mnie Pani i Pani Eta to Alfa i Omega.

23 sie 22:20
Eta:

23 sie 22:23
Radek:
1% tej wiedzy granice bym zrozumiał.
23 sie 22:25
Eta:
Radek dasz radę

......... trenuj rozwiązując dużo zadań.
23 sie 22:28
Radek:
Chciałbym rozwiązywać. Nawet szukam zbioru, żeby było dużo zadań ale nie umiem ich zrobić. I w
tym jest problem. Nie wiem czy to z powodu braku teorii czy wyleciało z głowy ?
23 sie 22:33
jakubs: Poszukaj w sieci: 310 przykladow granic z pelnymi rozwiazaniami krok po kroku
23 sie 22:35
23 sie 22:37
Mila:
Łatwiejsze masz w Analiza 1 Skoczylas Gewert. Masz w pdf.
Jest wytłumaczone po kolei od łatwiejszych zadań do trudniejszych.
23 sie 22:40
Radek:
Mam, tą książkę. Ok zajrzę do tego.
23 sie 22:51
Radek:
limn→∞(5−2n)=−∞
Jak to wykazać ? Który wzór ?
23 sie 23:35
Eta:
5 nie wpływa na wartość granicy ( za mała stosunku o 2n
2n → ...........
g=.........
23 sie 23:37
Eta:
miało być ...do 2n
23 sie 23:38
Radek:
Ma Pani jeszcze chwilkę czy już Pani idzie z forum ?
23 sie 23:46
Radek:
Czyli to by było tak:
[5−∞]=[−∞] jak bym rozpisał na boku ?
23 sie 23:47
Radek: ?
23 sie 23:56
jakubs: Tak
23 sie 23:59


 Tylko w ogóle nie potrzebne
Tylko w ogóle nie potrzebne
 Tak.
Tak.

 Hej Mila, Piotr10, jakubs, bezendu
Hej Mila, Piotr10, jakubs, bezendu  .
.

 Witam i dobranoc wszystkim, nic już nie myślę.
Radek , poznaj sie na wolframie, pomaga , możesz tam sprawdzać obliczone wyniki.
Witam i dobranoc wszystkim, nic już nie myślę.
Radek , poznaj sie na wolframie, pomaga , możesz tam sprawdzać obliczone wyniki.
 |cos(2x+1)|≤1 patrz na wykres.
|cos(2x)|≤1
|cos(2x+1)|≤1 patrz na wykres.
|cos(2x)|≤1
 1) sin0=0
sin(π)=0
sin(2π)=0 przecież znasz te podstawowe wartości.
2) rysowanie funkcji sin(nx) przecież też miałeś w szkole.
a) y=sin(1*x) patrz wykres.
b) [z[y=sin(2x)] zagęszczenie wykresu
c) y=sin(3x)
Jak widzisz wartości są w przedziale <−1,1>
1) sin0=0
sin(π)=0
sin(2π)=0 przecież znasz te podstawowe wartości.
2) rysowanie funkcji sin(nx) przecież też miałeś w szkole.
a) y=sin(1*x) patrz wykres.
b) [z[y=sin(2x)] zagęszczenie wykresu
c) y=sin(3x)
Jak widzisz wartości są w przedziale <−1,1>

 Powodzenia na "treningach"
Powodzenia na "treningach" 




 ......... trenuj rozwiązując dużo zadań.
......... trenuj rozwiązując dużo zadań.
