| a−b | 6p(3) − 2√3 | |||
przyprostokatna zawarta w podstawie ma dlugosc | = | } | ||
| 2 | 2 |
| h | ||
kat ostry np. z sinusa: sin α = | , drugi kat ma miare (180 − α) | |
| c |
| x | ||
masz ctg 30 = | , cos 30 = x/c | |
| h |
 KUZDE z Twojej wypowiedzi:
"Trapez jest opisany na okręgu zatem jest równoramienny (...)" wynika, że każdy trapez opisany
na okręgu jest równoramienny. Błąd logiczny.
Z treści zadania wiesz, że jest to trapez równoramienny. Nie czepiam się, tylko zwracam uwagę
na błąd we wniosku, wynikającym z Twojego zapisu w zdaniu przytoczonym.
Masz przykład trapezu opisanego na okręgu, który nie jest równoramienny, a nie spełnia Twojego
zdania: "Trapez jest opisany na okręgu zatem jest równoramienny (...)"
KUZDE z Twojej wypowiedzi:
"Trapez jest opisany na okręgu zatem jest równoramienny (...)" wynika, że każdy trapez opisany
na okręgu jest równoramienny. Błąd logiczny.
Z treści zadania wiesz, że jest to trapez równoramienny. Nie czepiam się, tylko zwracam uwagę
na błąd we wniosku, wynikającym z Twojego zapisu w zdaniu przytoczonym.
Masz przykład trapezu opisanego na okręgu, który nie jest równoramienny, a nie spełnia Twojego
zdania: "Trapez jest opisany na okręgu zatem jest równoramienny (...)"
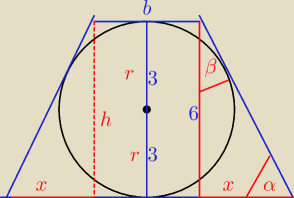 a) a = 6√3 b = 2√3
h = 2 *r = 2* 3 = 6
Pole trapezu P = 0,5 ( a + b)*h = 0,5 *( 6√3 + 2 √3)*6 = 3*8√3 = 24√3 [ cm2 ]
a) a = 6√3 b = 2√3
h = 2 *r = 2* 3 = 6
Pole trapezu P = 0,5 ( a + b)*h = 0,5 *( 6√3 + 2 √3)*6 = 3*8√3 = 24√3 [ cm2 ]
| a − b | 6√3 − 2√3 | |||
a = x + b + x ⇒ 2x = a − b ⇒ x = | = | = 2√3 | ||
| 2 | 2 |
| 6 | 6 | 2*3 | ||||
tg α = | = | = | = √3 , więc α = 60o | |||
| x | 2√3 | 2 √3 |
 Można i tak:
a)
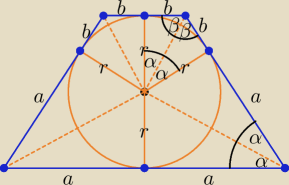
Środek okregu wpisanego to punkt przecięcia dwusiecznych kątów wewnętrznych,
r = 3, 2a = 6√3 ⇒ a = 3√3, 2b = 2√3 ⇒ b = √3
Można i tak:
a)
Środek okregu wpisanego to punkt przecięcia dwusiecznych kątów wewnętrznych,
r = 3, 2a = 6√3 ⇒ a = 3√3, 2b = 2√3 ⇒ b = √3
| 6√3 + 2√3 | ||
Pole trapezu P = | * 6 = ... | |
| 2 |
| r | 3 | 1 | ||||
tgα = | = | = | ⇒ α = 30o ⇒ 2α = 600, 2β = 180o − 60o = | |||
| a | 3√3 | √3 |
 b)
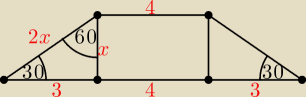
Z własności trójkąta prostokątnego, którego miara kata ostrego jest rowna 30o otrzymujemy:
x√3 = 3 ⇒ x = √3
b)
Z własności trójkąta prostokątnego, którego miara kata ostrego jest rowna 30o otrzymujemy:
x√3 = 3 ⇒ x = √3