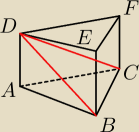
 Dany jest graniastosłup prawidłowy trójkątny o krawędzi podstawy długości 6 pole przekroju BCD=
18. Oblicz objętość graniastosłupa oraz cosinus kąta BCD
Dany jest graniastosłup prawidłowy trójkątny o krawędzi podstawy długości 6 pole przekroju BCD=
18. Oblicz objętość graniastosłupa oraz cosinus kąta BCD
| 1 | ||
P= | *a*h IDBI2=32+62=√45 | |
| 2 |
| 1 | ||
18= | *6*h | |
| 2 |
| MC | 3 | 1 | √5 | |||||
cos(∡BCD)= | = | = | = | taki kąt masz w treści na początku. | ||||
| DC | 3√5 | √5 | 5 |
 dziękuję
Ci Milu że tak dużo czasu poświęcasz pomaganiu innym
dziękuję
Ci Milu że tak dużo czasu poświęcasz pomaganiu innym 

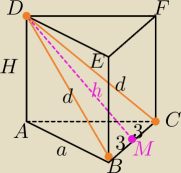
 Wynik to cos∡(BDC)=0,6
Milu mam podobne zadanie wyliczone wszystko tylko nie zgadza mi się wynik. Mogłabyś "rzucić"
okiem?
Wynik to cos∡(BDC)=0,6
Milu mam podobne zadanie wyliczone wszystko tylko nie zgadza mi się wynik. Mogłabyś "rzucić"
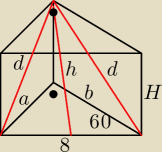
okiem?  Podstawą graniastosłupa prostego jest trójkąt prostokątny o przeciwprostokątnej długości 8 i
jednym z kątów 60o. Przez przeciwprostokątną dolnej podstawy i wierzchołek kąta prostego
górnej podstawy przeprowadzono płaszczyznę. W przekroju otrzymano trójkąt o polu równym
16√3. Oblicz objętość tego graniastosłupa.
Podstawą graniastosłupa prostego jest trójkąt prostokątny o przeciwprostokątnej długości 8 i
jednym z kątów 60o. Przez przeciwprostokątną dolnej podstawy i wierzchołek kąta prostego
górnej podstawy przeprowadzono płaszczyznę. W przekroju otrzymano trójkąt o polu równym
16√3. Oblicz objętość tego graniastosłupa.
| 1 | ||
P= | ah | |
| 2 |
| a | ||
sin60= | ||
| 8 |
| √3 | a | ||
= | |||
| 2 | 8 |
| b | ||
cos60o= | ||
| 8 |
| 1 | b | ||
= | |||
| 2 | 8 |
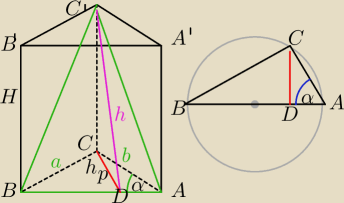 W porzednim zadaniu cos∡(BDC)=0,6 − dobrze obliczyłeś.
W zadaniu z 16:42
α=600
b=4, a=4√3
W ΔABC:
h=4√3
==========
Dalej :
ΔABC' nie jest trójkątem równoramiennym.
Spodek wysokości h pokrywa się ze spodkiem wysokości podstawy (hp) poprowadzonej z wierzchołka
C.
Oblicz hp=CD− wysokość ΔABC i z tw. Pitagorasa H ,
jeśli nie będzie się zgadzało z odpowiedzią to pisz.
W porzednim zadaniu cos∡(BDC)=0,6 − dobrze obliczyłeś.
W zadaniu z 16:42
α=600
b=4, a=4√3
W ΔABC:
h=4√3
==========
Dalej :
ΔABC' nie jest trójkątem równoramiennym.
Spodek wysokości h pokrywa się ze spodkiem wysokości podstawy (hp) poprowadzonej z wierzchołka
C.
Oblicz hp=CD− wysokość ΔABC i z tw. Pitagorasa H ,
jeśli nie będzie się zgadzało z odpowiedzią to pisz.
 dziękuję
dziękuję
