trygo ichtiolog: cosα=√{2}−1. Oblicz sinα i tgα

Bogdan: czy kąt jest kątem ostrym, to znaczy czy α∊(0^o 90^o) ?

PW: cosα = √2 − 1?

ichtiolog: Tak, kąt owy jest kątem ostrym

ichtiolog: to jest podwójny pierwiastek tzn. te nawiasy to jest 2 pierwiastek

PW: A, czyli √√2 − 1?

ichtiolog: O tak właśnie, tylko nie udało mi sie tak ładnie tego zapisać

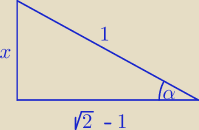
Bogdan: jesli α∊(0^o, 90^o) to x = ... (korzystamy z twierdzenia Pitagorasa)

	x
tgα =
	√2 − 1

ichtiolog: ale tu chodzi o konkretną wartość liczbową

aa: Na kalkulatorze oblicz ile wynosi ten pierwiastek i w tablicach znajdź jaki to jest kąt i odczytaj wartości dla sinusa i tangensa.

Bogdan:

	x
Oblicz wartość x z twierdzenia Pitagorasa i potem sinα = x oraz tgα =
	√2 − 1

i będziesz miał konkretną wartość liczbową, rachunki sam wykonaj.

PW: Masz konkretne wartości liczbowe, Bogdan podał sposób liczenia, tylko wziął √2 − 1 zamiast √√2−1. Z twierdzenia Pitagorasa x² + (√√2−1)² = 1² x² + √2 − 1 = 1 x² = 2 − √2 x = √2 −√2. Teraz stosuj definicje:

	x		x
sinα =		, tgα =
	1		√√2 − 1

pigor: ..., lub np. tak : α − kąt ostry , to mamy kolejno : cosα= √√2−1 ⇒ cos²α= √2−1 ⇒ 1−sin²α= √2−1 ⇒

	sin2α
⇒ sin2α=2−√2 ⇒ sinα= √2−√2 ⇒ tg2α=		=
	cos2α

	2−√2		(2−√2)(1+√2
=		=		=2+2√2−√2−2=√2 ⇒ tgα=4√2.
	√2−1		2−1

PW: Bogdanie, biorę wersję z 18:25.

Bogdan: Wziąłem wartość √2 − 1, ale można oczywiście wziąć inną wartość i przy okazji pozdrawiam stałych bywalców forum

opek: no i dziękuję panowie