Geometria analityczna Małgosia: Na wycinku paraboli y=x² − 6x + 5(pomiędzy jej pierwiastkami)wskazać punkt,który wraz z punktami A(1;1),B(4:7) utworzy trójkąt o możliwie największym polu

daras: a pierwiastki już masz ?

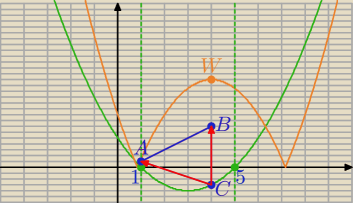
Bogdan: Szkic rozwiązania (bez szczegółowych rachunków, które zostawiam Małgosi. zielony wykres: y = x² − 6x + 5 pomarańczowy wykres: y = |1,5x_c² − 12x + 9| A = (1, 1), B = (4, 7) Miejsca zerowe paraboli y = x² − 6x + 5 to: x₁ = 1, x₂ = 5 Szukamy punktu C = (x_c, x_c² − 6x + 5) leżącego na tej paraboli przy czym 1 < x_c < 5 Wyznaczamy współrzędne wektorów (pomijam znak strzałki nad oznaczeniem wektora): CA = [x_c − 1, x_c² − 6x_c + 4] CB = [x_c − 4, x_c² − 6x_c − 2] | x_c − 1 x_c² − 6c + 4| Pole trójkata P = 0,5 * | | | | = |1,5x_c² − 12x + 9| | x_c − 4 x_c² − 6x − 2| Funkcja f(x) = |1,5x_c² − 12x + 9| osiąga największą wartość w wierzhołku W = (4, 15), czyli dla x = 4 Wobec tego C = (4, 4² − 6*4 + 5) = (4, −3)

daras:

daras: Małgosiu zrozumiałaś? bo widze , że jesteś i podziwiasz

daras: chyba nie , bo nawet nie podziękowałaś