fnkcja liniowa linia: Wyznacz wszystkie liczby k, dla ktorych wykres funkcji liniowej f jest nachylony do osi OX pod kątem α, jeśli: a) f(x)=(2k−3)x+ k, α∊(90o , 135o > b)f(x)=2k−kx, α∊<120o ,180o )

PW: a) f(x) = (2k−3)x +k Liczba (2k−3) − współczynnik kierunkowy prostej − jest tangensem kąta nachylenia, to znaczy 2k−3 = tgα. Skoro α∊(90°, 135°), to tgα∊(−∞, 1) − tu warto narysować wykres funkcji tangens, by zobaczyć skąd się to wzięło). Tym samym 2k−3∊(−∞, 1), czyli 2k−3 < 1 k < 2.

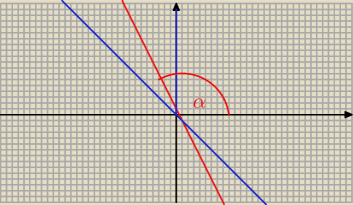
Janek191: f(x) = a x + b , to a = tg α a ) α ∊ ( 90^o ; 135^o > tg 135^o = − 1 i tg α < − 1 więc a ∊ ( − ∞ ; − 1 > − − − − − − − − − − − − − Mamy f(x) = ( 2 k − 3) x + k więc a = 2 k − 3 zatem 2 k − 3 ∊ ( − ∞ ; − 1> 2 k − 3 > − ∞ i 2 k − 3 ≤ − 1 k > − ∞ i k ≤ 1 Odp. k ∊ ( − ∞ ; 1 > =================

J: I kto ma rację ... .... obstawiam Janka...

PW: Tak! Rąbnąłem się − radziłem narysować wykres tangensa, a sam tego nie zrobiłem i wydało mi się, że tgα∊(−∞,1) zamiast − jak słusznie pisze Janek191 , tgα∊(∞,−1).

linia: nie rozumiem skąd się to wzięło α ∊ ( 90o ; 135o > tg 135o = − 1 i tg α < − 1 więc a ∊ ( − ∞ ; − 1 > − − − − − − − − − − − −

PW: Na przedziale (90°, 180°) funkcja tangens jest rosnąca i przyjmuje wartości od −∞ do 0 ( po drodze jest tg135°, czyli −1). Naprawdę warto to narysować. −∞ < tgα < −1 dla α∊(90°, 135°), to znaczy −∞ < a < −1. Nasze a to tgα = (2k−3).

Mila: To może ja narysuję.