romb dawek: Punkty A=(−1,−6) i B=(3,−3) są kolejnymi wierzchołkami rombu ABCD. Wierzchołek C należy do prostej o równaniu x+y=5. Znajdź współrzędne punktów C i D.

Ja: C=(x, 5−x) i licz

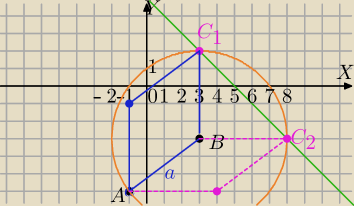
Mila: A=(−1,−6) i B=(3,−3) k: x+y=5, ⇔y=−x+5 a=|AB|=√4²+3²=5 W rombie wszystki boki sątej samej długości. kreślimy okrąg o promieniu r=5 i środku w punkcie B (x−3)²+(y+3)²=25 Otrzymujemy dwa punkty przecięcia z prostą. Obliczamy : (x−3)²+(−x+5+3)²=25 x²−6x+9+x²−16x+64=25 2x²−22x+48=0 /:2 x²−11x+24=0 Δ=121−96=25

	11−5		11+5
x=		lub x=
	2		2

x=3 lub x=8 y=−3+5=2 lub y=−8+5=−3 C₁=(3,2) C₂=(8,−3) szukaj punktu D₁ i D₂