Zbiory
Paulina:
Rachunek zbiorów
Niech A={2n−1: n∊N} B={6n+1: n∊N}
Znajdź A∪B A∩B A\B B\A
Jak to zrobić ?
19 sie 21:25
Kacper: Oa początek wypisz po kilka liczb i patrz

19 sie 21:32
Paulina:
Ok.
Dla a mam o jedną mniej ? w b o 6 więcej ?
19 sie 21:33
Mila:
Wypisz kilka początkowych wyrazów każdego ze zbiorów, a zauważysz pewną zalezność między
zbiorami.
19 sie 21:33
5-latek: Chyba cos te zbiory A i b przepisalas zle bo np
A =2n−1 i n nalezy do naturalnych
to mamy ponoc teraz 0 nalezy do naturalnych to mamy 2*0−1=−1 ,, 2*1−1=1 2*2−1=3 ale za n
mozemy wstawic oo i dostaniemy co 2*oo−1= oo−1=oo .Moze jest jakis przedzial do ktorego
nalezy n
Moze to o to chodzi ze bedzie to przedzial <−1,oo) ale to musi sie jeszce ktos wypowiedziec
19 sie 21:33
Paulina:
Wypisuję elementy dla zbioru:
A={−1,1,2,3,,4,5,6...}
B={1,7,13,19}
B−wychodzą liczb pierwsze ewidentnie.
19 sie 21:43
zombi: Zauważ, że
6n+1 = 2(3n+1) − 1
wobec tego zbiór B⊆A
Tak więc od razu mamy A∩B = {6n+1: n∊N}, natomiast AuB = {2n−1; n∊N}
19 sie 21:45
Eta:
A= {−1,1,3,5,7,9,........ }
B={1,7,13,19,..........}
AUB=A
A∩B=B
A\B=....
B\A=........
19 sie 21:45
zombi: B={1,7,13,19,25,...}
19 sie 21:46
Kacper: I nie wolno ulegać intuicji bo dla n=20 mamy 121. Czy to jest liczba pierwsza?

19 sie 21:46
5-latek: Sprawdz jeszce raz u siebie elementy zbioru A . Ja tam no nie widze w tym zbiorze 2 czy np 4
czy np 6
19 sie 21:47
Paulina:
Na pierwszy rzut oka wydawało się inaczej...
A\B=tu jest trochę bez sensu... bo nie da się jednoznacznie określić takich elementów
B\A=∅
19 sie 21:48
Kacper: Oczywiście że ich nie ma bo to podzbiór liczb nieparzystych
19 sie 21:50
Eta:
A\B= wszystkie, które są nieparzyste{−1 .........} i z dzielenia przez 6 nie dają reszty 1
19 sie 21:50
Mila:
Pochopny wniosek co do B.
B={1,7,13,19,25,31, 37,43, 49,55......}
Każda z tych liczb jako nieparzysta znajduje się w zbiorze A.
B⊂A
A∪B=A złączenie zbiorów
A∩B=B część wspólna
B\A=Φ to co należy do B i nie należy do zbioru A
A\B kombinuj
19 sie 21:51
zombi: Możesz zapisać A\B jako sumę zbiorów np A\B = A1uA2, gdzie
A1 = {−1,5,11,17...}
A2 = {3,9,15,...}
19 sie 21:52
19 sie 21:54
Paulina:
A\B= nie wiem jak to bo wypisanie początkowych elementów nic nie daję.
19 sie 21:55
Paulina:
czytaj tu ten link jest mało przydatny, aż wcale..
To miałam w liceum a teraz są studia...
19 sie 21:56
19 sie 21:56
Kacper: Ale autor zapewne chce prosto i krótko. Wystarczy zapisać to co podała Eta za pomocą symboli

19 sie 21:57
zombi: Jeszcze tak łatwiej możesz to znaleźć, wiemy, że A = {2n−1, n∊N}, A tworzą wszystki liczby
nieparzyste, natomiast B = {6n+1, n∊N}, czyli liczby które ≡ 1 (mod 6), a my chcemy A\B, czyli
liczby nieparzyste, które dają resztę ≠ 1 przy dzieleniu przez 6. Są tylko dwie możliowści
6n+3 i 6n+5 i suma tych zbiorów jest naszą różnicą A\B.
19 sie 22:00
Paulina:
A co to ma do moich zadań ? To co wstawiłaś to poziom lo... Wiem jak wyznaczać część wspólną
itp dla konkretnych przedziałów.. Może czytaj ze zrozumieniem moje pytanie. ?
19 sie 22:01
Eta:

19 sie 22:01
Paulina:
Czyli tak jak napisała Eta będzie poprawnie ? Profesor uzna to na kolokwium ?
19 sie 22:03
zombi: Przecież możesz tak też zapisać i wygląda ładnie
A\B = A1∪A2, gdzie A1 = {6n+3, n∊N}, A2 = {6n−1, n∊N}
19 sie 22:04
Paulina:
Ale Ty teraz ze zbioru A zrobiłeś dwa podzbiory.. Chodzi o najprostszy sposób

19 sie 22:06
zombi: Ale nie upchniesz tego w jeden, chyba, że chcesz na chama:
A\B = {−1,3,5,9,11,15,17,...}
19 sie 22:08
zombi: Ale jaki tam porządek to nie widać.
19 sie 22:08
Eta:
@Paulina
Zapisz tak ,jak podaje zombi
Ja podałam słownie: wszystkie nieparzyste z −1 i takie, które z dzielenia przez 6
nie dają reszty 1
6n+2 i 6n+4−−− odpadają ,bo parzyste
zostają 6n+3 i 6n+5= 6n−1( bo w tym zbiorze masz −1
zatem: A\B={6n+3 lub 6n−1 : n∊N}
i to wszystko
19 sie 22:13
Paulina:
0∊N tak mam podane w pdfie.
A\B={liczby podzielne przez 3 i liczby które przy dzieleniu przez 3 dają resztę 2 }
19 sie 22:13
Eta:
Widzę,że "tłoczno " się zrobiło ...... ( więc spadam

19 sie 22:14
Paulina:
Nigdzie nie spadaj !
19 sie 22:18
Paulina:
To samo polecenie:
A={2n−1: n∊N}
B={4n : n∊N}
A={−1,1,2,3,4....}
B={0,4,8,12,16...}
A∪B=A
A∩B=B
A\B={4n+1, ?}
B\A={0}
19 sie 22:21
Paulina:
Mila czemu określone dla n≥1 ?
19 sie 22:21
zombi: A∪B=N
A∩B=∅
A\B=A
B\A=B
19 sie 22:23
zombi: oczywiście
A∪B = N∪{−1}
19 sie 22:24
Paulina:
A∪B nie może być naturalne ! przecież zbiór A={−1....}
czemu A∩B zbiór pusty skoro w zbiorze A występuję liczby podzielne przez 4 ?!
19 sie 22:29
zombi: A={2n−1} − same nieparzyste
B={4n} − same parzyste, to oczywiste, A∩Bzbiór pusty
19 sie 22:33
zombi: Czytasz co napisałem
AuB = Nu{−1}
19 sie 22:33
Paulina:
Dobra ja się zgapiłam...
19 sie 22:33
zombi: Mila,Z Etą podaliśmy podaliśmy odpowiedź.
19 sie 22:43
Paulina:
22:21 ?
20 sie 10:07
Paulina: 
20 sie 16:32
Mila:
Niech A={2n−1: n∊N} B={4n: n∊N}
Znajdź A∪B, A∩B ,A\B, B\A
A={−1,1,3,5,7,9,11,13,....}
B={0,4,8,12,16,....}
1)A∩B=Φ zbiory są rozłączne
2) A∪B − złączenie zbiorów
AUB=(N∪{−1})\C
a) Ze zbioru :
(N∪{−1}) należy wyłączyć elementy zbioru C={4n+2: n∊N}
C={6,10,14,18,.....}
b) Wydaje mi się, że można wypisać elementy zbioru A∪B
A∪B={−1,0,1, 3,4,5, 7,8,9, 11,12,13, 15,16,17,......}
tu można pomyśleć nad zbiorczym zapisem.
3)A\B=A
4)B\A=B
20 sie 16:47
Paulina:
Dziękuję
Mila 
20 sie 17:44
Mila:
I dalej pracuj, wyznaczniki porzuciłaś?
20 sie 17:44
Paulina:
Tak, na razie zajęłam się trochę innymi rzeczami. Pierwsze co muszę zrobić to Rachunek Zbiorów

20 sie 18:29
Paulina:
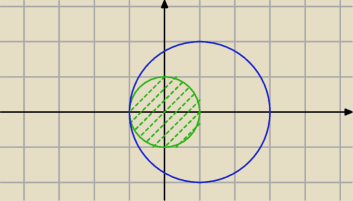
Podaj interpretacje geometryczną zbiorów
A={(x,y)∊R
2 x
2+y
2≥1}
B={(x,y)∊R
2 x
2−2x+y
2≤3}
Zielony to koło x
2+y
2≥1
Niebieski to okrąg (x−1)
2+y
2≤4
S=(1,0) r=2
I jak teraz ?
20 sie 18:45
Mila:
x2+y2≥1 punkty płaszczyzny na zewnątrz okręgu, łącznie z okręgiem.
(x−1)2+y2≤4 koło, punkty wewnątrz okręgu, łącznie z okręgiem
I co masz zrobić z tymi zbiorami?
20 sie 18:52
Paulina:
A∪B
A∩B
A\B
B\A
20 sie 18:52
Paulina:

A=okrąg
B=koła
A\B=∅
A∪B=(x−1)
2+y
2≤4
A∩B=x
2+y
2≥1
B\A= ?
20 sie 18:56
Mila:
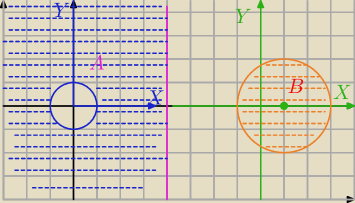
20 sie 19:03
Paulina:
Czemu okrąg mam źle ?
20 sie 19:11
Paulina:
Ale wtopa tam nie jest nierówność a ja traktuje jako okrąg.. Przepraszam
20 sie 19:14
Paulina:
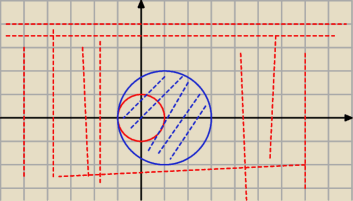
A=x
2+y
2≥1
B=(x−1)
2+y
2≤4
A∪B= jak opisać całą płaszczyznę
A∩B=x
2+y
2≥1
A\B=?
B\A= ?
20 sie 19:32
Kacper: R2 płaszczyzna
20 sie 19:45
Paulina:
A∪B=R2
A\B= ?
B\A=?
20 sie 19:50
Mila:
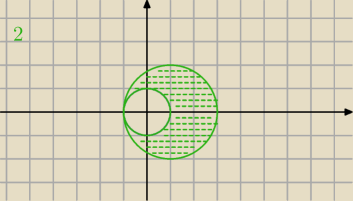
2)A∩B − zielony obszar
20 sie 19:51
Paulina:
Ale jak to opisać ?
20 sie 19:55
Mila:
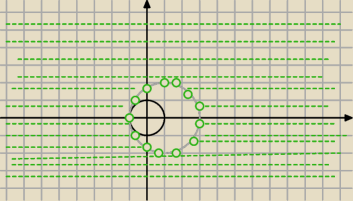
3) A\B− zielony obszar
20 sie 19:56
Mila:
Masz podać interpretację geometryczną, czyli ilustrację.
B|A narysuj sama.
20 sie 19:58
Paulina:

Chyba zrezygnuję z tej matmy na UJ i zostanę tylko na AGH..
20 sie 20:04
Mila:
Co to jest?
20 sie 20:15
Mila:
Oj, zaraz zrezygnuję, przecież tam będą Cię uczyli rozumowania.
20 sie 20:21
Paulina:
B\A
20 sie 20:23
Mila:

20 sie 20:25
Paulina:
A\B ? Moja wersja ?
20 sie 20:26
Mila:
O której godzinie wpis?
20 sie 20:33
Paulina: 20:04
20 sie 20:34
Mila:
Podałam Ci A\B o godzinie 19:56.
A\B=A\(A∩B) to przecież wiesz , chociażby z rachunku prawd., tam często korzystało się z tej
równości.
20 sie 20:39
Paulina:
Dziękuję po raz kolejny..
20 sie 20:54









 Podaj interpretacje geometryczną zbiorów
A={(x,y)∊R2 x2+y2≥1}
B={(x,y)∊R2 x2−2x+y2≤3}
Zielony to koło x2+y2≥1
Niebieski to okrąg (x−1)2+y2≤4
S=(1,0) r=2
I jak teraz ?
Podaj interpretacje geometryczną zbiorów
A={(x,y)∊R2 x2+y2≥1}
B={(x,y)∊R2 x2−2x+y2≤3}
Zielony to koło x2+y2≥1
Niebieski to okrąg (x−1)2+y2≤4
S=(1,0) r=2
I jak teraz ?
 A=okrąg
B=koła
A\B=∅
A∪B=(x−1)2+y2≤4
A∩B=x2+y2≥1
B\A= ?
A=okrąg
B=koła
A\B=∅
A∪B=(x−1)2+y2≤4
A∩B=x2+y2≥1
B\A= ?

 A=x2+y2≥1
B=(x−1)2+y2≤4
A∪B= jak opisać całą płaszczyznę
A∩B=x2+y2≥1
A\B=?
B\A= ?
A=x2+y2≥1
B=(x−1)2+y2≤4
A∪B= jak opisać całą płaszczyznę
A∩B=x2+y2≥1
A\B=?
B\A= ?
 2)A∩B − zielony obszar
2)A∩B − zielony obszar
 3) A\B− zielony obszar
3) A\B− zielony obszar
 Chyba zrezygnuję z tej matmy na UJ i zostanę tylko na AGH..
Chyba zrezygnuję z tej matmy na UJ i zostanę tylko na AGH..
