log magda: Określ dziedzinę funkcji f(x)=log₂ x/x−1

magda: jak to zrobić?

Aza:

	x
D:		>0 i x ≠1
	x−1

rozwiązujemy nierówność: x( x −1) >0 => x€( −∞, 0) U ( 1, ∞) i x≠1 więc: D_f = (−∞, 0) U ( 1,∞)

magda: w odp. jest x∊(0,1)

Aza: To źle jest w odpowiedzi widać "gołym okiem"

magda: sory to ja żle podałam x/1−x −−− tak ma być

Aza: Uzasadniam: wybierasz np x = ¹₂ z tego przedziału , który masz w Twojej odp:

	0,5		0,5
otrzymasz :		=		= −1 ... sprzeczność
	0,5 −1		−0,5

bo liczba logarytmowana musi być > 0

Aza: No to dziecino? ........ poprawny zapis .... daje poprawną odp popraw juz sama to teraz proste ramiona paraboli : x( 1 −x) −−− zwrócone do dołu więc x( 1−x) >0 => x€............. podaj rozwiązanie i teraz będzie "git"

magda: ale ja nie rozumiem dlaczego taki przedział (0,1)

Aza: zaraz Ci narysuję

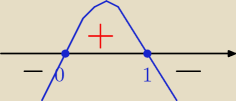
Aza: Omg x(1 −x) >0 => x€ (0,1) miejsca zerowe x = 0 v x = 1 parabola ramionami do dołu bo x *(−x) = −x² więc wartości dodatnie ( >0 ) nad osiąOX czyli x€ (0, 1)

magda: dziękuję już rozumiem

rozkminiacz90: F(x)=logx+1(4−x2)

bezendu: x+1 jest w podstawie ?

bezendu: Zakładam, że to powinno być tak a Ty źle przepisałeś f(x)=log_x+1(4−x²) x+1>0 ∧ x+1≠1 ⋀ x²−4<0 x>−1 x≠0 x∊(−1,∞) Teraz rozważ te warunki które podałem, i następnie część wspólna tych warunków.

Bella: określ dziedzinę funkcji : a) f(x) = log_|2−x|[(1/4)^x2−10 −4] b) f(x) = √log_1/2(4−x)+1