
| 1 | ||
sinx2≥0 v (sinx−1)2 ≥0 v sinx+ | ≥0
| |
| 2 |
| 1 | ||
sinx≥0 v sinx≤0 v sinx−1≥0 v sinx−1≤0 v sinx≥− | ||
| 2 |
| π | π | |||
x=2kπ x= | +2kπ x=− | +2kπ v | ||
| 2 | 6 |
| 7π | ||
+2kπ
| ||
| 6 |
 Godzio
Godzio  można też tak:
sinx = t
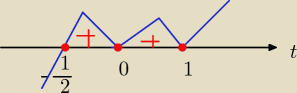
t2(t −1)2(t+12) ≥0
t€ < −12, 1> => −12≤sinx ≤1
teraz już można odczytać x €.......
Dobranoc
można też tak:
sinx = t
t2(t −1)2(t+12) ≥0
t€ < −12, 1> => −12≤sinx ≤1
teraz już można odczytać x €.......
Dobranoc 