Geometria Blue: Boki AC i AB trójkąta ABC mają długości odpowiednio b i c. Dwusieczna kąta A przecina bok BC w punkcie D takim, że |AD| = |BD|. Oblicz długość boku BC.

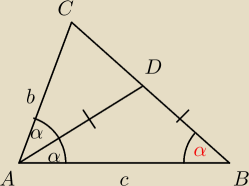
Kacper: no to masz rysunek Teraz próbuj sama na początek powypisuj wszystkie brakujące kąty i obserwuj

Blue: no właśnie rysunek zrobiłam i pozostałe kąty to 2α, 180 −2α i 180 − 3α, ale nie wiem, co dalej ....:c

Blue: a bo te trójkąty są podobne...

dyzio: ∠ADB = 180 − 2α |AD| = |DB| = x Tw. sinusów

x		c
	=
sinα		sin(180 − 2α)

xsinα = 2csinα / sinα x = 2c Nie wiem czy dobrze, ale do takich wniosków doszedłem

Kacper: dyzio skąd masz taką linijkę? xsinα = 2csinα / sinα

dyzio: ma być xsinα = csin2α ?

Kacper: ja to widzę tak: xsin2α=csinα Ale może potrzebuje okularów

dyzio: a sorki rzeczywiście A co dalej byś z tym zrobił ?

bezendu: Taka jest odpowiedź ? BC=√b(b+c)

Blue: tak taka Ja już znalazłam inne rozwiązanie (znowu wykorzystujące tw o dwusiecznej) i podobieństwo trójkątów. Muszę zapamiętać wreszcie to tw. o dwusiecznej

Paulina: Skoro w treści jest informacja o dwusiecznej to chyba narzuca się, że trzeba skorzystać z tego twierdzenia.....