pole dawek: Dane są punkty A=(1,−1) i B=(3,3) oraz prosta k o równaniu y=x+3. Wyznacz na prostej k taki punkt C, aby pole trójkąta ABC było równe 6.

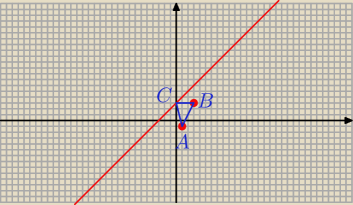
Janek191: A = ( 1; − 1) B = ( 3; 3) więc I AB I = √( 3 − 1)² + ( 3 − (−1))² = √20 = 2√5 Prosta AB y = a x + b − 1 = a + b 3 = 3a + b −−−−−−−−−−−−−−−− 4 = 2a a = 2 b = − 1 − a = − 3 y = 2 x − 3 2 x − y − 3 = 0 ← równanie prostej AB −−−−−−−−−−−−−−−−− C = ( x₀ ; y₀) = ( x₀; x₀ + 3) − bo leży na prostej o równaniu y = x + 3

	6
P = 0,5 I AB I *h = 0,5*2√5*h = √5*h = 6 ⇒ h =
	√5

więc

I 2*x0 − 1*(x0 + 3) − 3 I		6
	=
√22 + (−1)2		√5

I x0 − 6 I		6
	=
√5		√5

I x₀ − 6 I = 6 x₀ = 0 lub x₀ = 12 więc y₀ = 0 + 3 = 3 lub y₀ = 12 + 3 = 15 zatem C = ( 0; 3) lub C = ( 12; 15 ) =========================

pigor: ... lub np. tak : A=(1,−1), B=(3,3) i niech C= (x,y)=(x,x+3)=? (*), to CA^→= [1−x, −1−x−3]= [1−x , −4−x] , CB^→= [3−x,3−x−3] = [3−x , −x] , więc P_ΔABC=¹₂|CA^→x CB^→|= ¹₂|(1−x)(−x)−(−4−x)(3−x)|= = ¹₂|−x+x²+12+3x−4x−x²|= ¹₂|−2x+12| ⇒ P_Δ=6 ⇔ ⇔ |−x+6|=6 ⇔ |x−6|=6 ⇔ x−6=−6 v x−6=6 ⇔ ⇔ x=0 v x=12 ⇒ stąd i z (*) C=(0,3) v C=(12,5) .

Eta: C(12,15) bo 12+3= ........

Gustlik: Najprościej wyznacznikiem wektorów: A=(1,−1) B=(3,3) C=(x, x+3) AB^→=[3−1, 3−(−1)]=[2, 4] AC^→=[x−1, x+3+1]=[x−1, x+4] d(AB^→, AC^→)= | 2 4 | | x−1 x+4 | =2(x+4)−4(x−1)=2x+8−4x+4=−2x+12

	1		1
P=		|d(AB→, AC→)|=		|−2x+12|=|x−6|
	2		2

|x−6|=6 x−6=6 v x−6=−6 x=12 v x=0 y=15 v y=3 C=(12, 15) v C=(0, 3)

Eta: Zobacz Gustlik rozwiązanie pigora

Gustlik: Ja wiem, ale lepiej to zapisać wyznacznikiem i mnożyć na krzyż, bardziej obrazowe i łatwo skojarzyć np. tym, co znają wyznacznikową metodę rozwiązywania układów równań, pigor to fajnie rozwiązał. Ja tylko chciałem wskazać na wyznacznik wektorów, bo tak się liczy iloczyn wektorowy.

Eta: