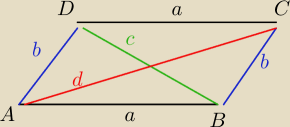
W zadaniu o treści:
W równoległoboku ABCD kąt rozwarty ABC ma miarę 120 stopni oraz IABI>IADI.
| IABI | ||
Wyznacz stosunek k, gdzie k= | , | |
| IADI |
| IDBI | 37 | |||
jeśli wiadomo, że | =√ | |||
| IACI | 79 |
| 3 | 1 | |||
Wyciągnąłem b2 przed nawias i wyszło mi k= | V k= 2 | . | ||
| 7 | 3 |
| 1 | ||
Dlaczego odpowiedź to tylko k= 2 |  | |
| 3 |
| 3 | 3 AB | |||
bo dla k= | jest | czyli w tym przypadku IABI < IADI. | ||
| 7 | 7 AD |
| 7 | 7 AB | |||
a dla k= | jest | , czyli zgodnie z założeniem IABI > IADI | ||
| 3 | 3 AD |
| 3 | IABI | 3 | ||||
Nie tak.... jeśli k = | , to | = | ⇔ 7IABI = 3IADI ... to znaczy,że | |||
| 7 | IADI | 7 |