f.kwadratowa
tyu:
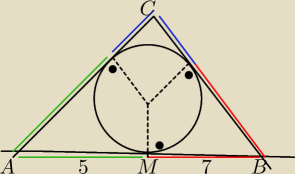
czy ktoś mógłby mi wytłumaczyć rozwiązanie do poniższego zadania.
W trójkąt ABC wpisano okrąg. Punkt styczności M z bokiem AB podzielił ten bok na odcinki o
dług. 5 i 7. Widząc że kwadrat pola trójkąta ABC jest równy 980, oblicz długości pozostałych
boków tego trójkąta.
znalazłem poniższe rozwiązanie tutaj
http://zadane.pl/zadanie/5686112
980=p(p−a)(p−b)(p−c)
980=(12+x)*x*5*7

skąd się wzięły te liczby
x
2+12x−28=0
Δ=144+112=256=16
2
x
1=−16 x
2=2
rys. znam te zależności o podziale boków trójką przez punkt styczności, ale nie wiem jak ten
wzór jest zastosowany.
Tutaj
http://forum.zadania.info/viewtopic.php?f=3&t=56154&p=212058 jest inny sposób, ale wychodzą mi jakieś dziwne liczby.
Nie wiem, czy tu mam najpierw wyliczyć x uzależniając od c, potem podstawić i obliczyć c.
Mila:
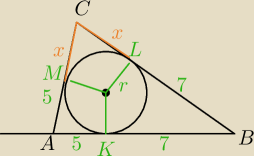
|AK|=|AM|=5
|KB|=|BL|=7
|CL|=|CM|=x, x>0
Te 3 równości wynikają z własności:
Punkty styczności okręgu wpisanego w kąt są jednakowo odległe od wierzchołka kąta.
===============================================================
Dalej masz skorzystane ze wzoru Herona
P
Δ=
√p*(p−a)*(p−b)*(p−c)
p=połowa obwodu trójkąta
p=7+5+x
P
2=980
P
2=(12+x)*(12+x−12)*(12+x−7−x)*(12+x−x−5)⇔
(12+x)*x*5*7=980 /:35
(12+x)*x=28
Jasne?
==========
tyu: Dziękuję
Mila. Właśnie przeliczam sobie, ale trzecia linia od dołu
...(12+x−7−x)*(12+x−x−5)

To jest ...(p−b)*(p−c)
czyli b=7+x i jeśli jest p−b, to 12+x−(7+x)= 12+x−7−x
czyli jasne

 czy ktoś mógłby mi wytłumaczyć rozwiązanie do poniższego zadania.
W trójkąt ABC wpisano okrąg. Punkt styczności M z bokiem AB podzielił ten bok na odcinki o
dług. 5 i 7. Widząc że kwadrat pola trójkąta ABC jest równy 980, oblicz długości pozostałych
boków tego trójkąta.
znalazłem poniższe rozwiązanie tutaj http://zadane.pl/zadanie/5686112
980=p(p−a)(p−b)(p−c)
980=(12+x)*x*5*7
czy ktoś mógłby mi wytłumaczyć rozwiązanie do poniższego zadania.
W trójkąt ABC wpisano okrąg. Punkt styczności M z bokiem AB podzielił ten bok na odcinki o
dług. 5 i 7. Widząc że kwadrat pola trójkąta ABC jest równy 980, oblicz długości pozostałych
boków tego trójkąta.
znalazłem poniższe rozwiązanie tutaj http://zadane.pl/zadanie/5686112
980=p(p−a)(p−b)(p−c)
980=(12+x)*x*5*7  skąd się wzięły te liczby
x2+12x−28=0
Δ=144+112=256=162
x1=−16 x2=2
rys. znam te zależności o podziale boków trójką przez punkt styczności, ale nie wiem jak ten
wzór jest zastosowany.
Tutaj http://forum.zadania.info/viewtopic.php?f=3&t=56154&p=212058 jest inny sposób, ale wychodzą mi jakieś dziwne liczby.
Nie wiem, czy tu mam najpierw wyliczyć x uzależniając od c, potem podstawić i obliczyć c.
skąd się wzięły te liczby
x2+12x−28=0
Δ=144+112=256=162
x1=−16 x2=2
rys. znam te zależności o podziale boków trójką przez punkt styczności, ale nie wiem jak ten
wzór jest zastosowany.
Tutaj http://forum.zadania.info/viewtopic.php?f=3&t=56154&p=212058 jest inny sposób, ale wychodzą mi jakieś dziwne liczby.
Nie wiem, czy tu mam najpierw wyliczyć x uzależniając od c, potem podstawić i obliczyć c.
 |AK|=|AM|=5
|KB|=|BL|=7
|CL|=|CM|=x, x>0
Te 3 równości wynikają z własności:
Punkty styczności okręgu wpisanego w kąt są jednakowo odległe od wierzchołka kąta.
===============================================================
Dalej masz skorzystane ze wzoru Herona
PΔ=√p*(p−a)*(p−b)*(p−c)
p=połowa obwodu trójkąta
p=7+5+x
P2=980
P2=(12+x)*(12+x−12)*(12+x−7−x)*(12+x−x−5)⇔
(12+x)*x*5*7=980 /:35
(12+x)*x=28
Jasne?
==========
|AK|=|AM|=5
|KB|=|BL|=7
|CL|=|CM|=x, x>0
Te 3 równości wynikają z własności:
Punkty styczności okręgu wpisanego w kąt są jednakowo odległe od wierzchołka kąta.
===============================================================
Dalej masz skorzystane ze wzoru Herona
PΔ=√p*(p−a)*(p−b)*(p−c)
p=połowa obwodu trójkąta
p=7+5+x
P2=980
P2=(12+x)*(12+x−12)*(12+x−7−x)*(12+x−x−5)⇔
(12+x)*x*5*7=980 /:35
(12+x)*x=28
Jasne?
==========
 To jest ...(p−b)*(p−c)
czyli b=7+x i jeśli jest p−b, to 12+x−(7+x)= 12+x−7−x
czyli jasne
To jest ...(p−b)*(p−c)
czyli b=7+x i jeśli jest p−b, to 12+x−(7+x)= 12+x−7−x
czyli jasne 
