sześcian, szescian, sfera KUZDE: Dany jest sześcian o krawędzi długości a. Oblicz promień sfery, do której należy środek symetrii sześcianu i która jest styczną do 3 ścian sześcianu.

daras:

	√2
r =		a
	2

KUZDE: Niestety nie

	a(3−√3)
odp.
	4

Ale mam straszny problem z wyobrazeniem danej sytuacji.

daras: narysuj sobie w rzucie prostokątnym, okrąg styczny do dwu ścian więc promień jest do nich prostopadły do nich, środek sfery leży na przekątnej, na pewno masz dobrą odp ?

Mila: Wyobraź sobie, że wrzucasz w róg sześcianu piłeczkę pingpongową, ona "dotyka " dna i dwóch ścianek bocznych.

KUZDE: Nie wiem czy odp. z ksiazki jest na pewno dobra, bo czesto mam pomylki w odp. z zadan, ktorych nie umiem. Jeszcze raz sprobuje rozwiklac jak radzicie.

KUZDE: Ja sie poddaje, ale gdyby ktos chcial umiescic swoje rozwiazanie bede wdzieczny. Chcialem policzyc co nie co w wakacje, ale po przeczytaniu nastepnych zadan.... To raczej kiepski pomysl

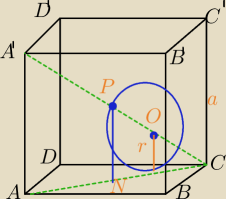
Mila: Kula styczna do ABCD, BCC'B', DCC'D"

	a√3
|PC|=
	2

	1
|PN|=		a
	2

|OC|=|PC|−r

PN		r
	=
PC		PC−r

Licz sam dalej.

Mila: Weź jabłko i wciśnij w jakiś kącik na biurku, albo zrób model sześcianu bez górnej podstawy i wszystko zrozumiesz.

lolo: odp jest dobra

Mila: Wiem.

daras: Mila ma rację tu trzeba bardziej stereo i wystarczy tw. Talesa a ja pojechałem z kątów,

	a√3(√3−1)
odpowiedź też dobra choc moznaby prosciej r =
	4

KUZDE: Super, dzieki wielkie ! W takim razie sprobuje przerobic jeszcze kilka zadan w tym miesiacu.

Mila: Wszystko jest łatwe, gdy się już rozwiąże.

daras: kilka zadań na miesiąc to w tempie żółwia a może dziennie?

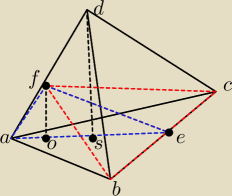
KUZDE: #2 W prawidłowym ostrosłupie trójkątnym płaszczyzna,zawierająca jedna z krawędzi podstawy i prostopadła do przeciwległej krawędzi bocznej, dzieli ostrosłup na dwa wielościany, których objętości są do siebie w stosunku 2:3. Wyznacz cosinus kąta płaskiego przy wierzchołku ostrosłupa. a− dl. krawędzi podstawy, b− dl. k. bocznych. lFOl / lDSl = 2/5 ( 2/2+3) Czerwony trojkat, to dana plaszczyna. Niebieski tr. jest prostakatny (kat AFE) i z tego licze lFEl

	2b		a√3
lFEl2 = (		)2 + (		)2
	5		2

	3b		a
lFEl2 + (		)2 = (hb)2 = b2 − (		)2
	5		2

	12b2		22
stad mam a2 =		=> (hb)2=		*b2
	25		25

cos² (α/2) = 22/25 cos a = 2cos² a/2 − 1 = (44 − 25 ) / 25 = 19/25 Dobrze ?

KUZDE: Do zadania wyzej:

	a√3		2b
lFEl2 = (		)2 − (		)2, pozniej do hb to zastosowac i wychodzi piekny wynik
	2		5

	3
		, a dla stosunku 3/5 wyjdzie 2/5.
	5

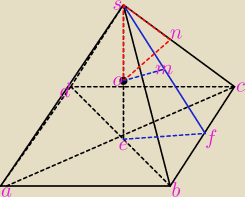
#3 W ostroslupie czworokatnym prawidlowym odleglosc srodka jego wysokosci od krawedzi i od jego sciany bocznej wynosza odpowiednio a i b. Wyznacz objetosc ostroslupa. H − dl. wysokosci ostr. c − dl. krawedzi podstawy Z podobienstwa trojkatow(zaraz dodam rysunek) mam takie proporcje:

H		√2H2 + c2		H		√4H2 + c2
	=		,		=
2a		c		2b		c

(Hc)² = 4a²(2H² + c²) = 4b²(4H²+c²) Ale z tego nic nie chce wyjsc !

KUZDE:

Mila: Jutro, jeśli nikt nie pomoże wcześniej. Dobranoc.

KUZDE: Oks, dzieki. Dobranoc

KUZDE: Juz mam, juz mam Zrobione !

daras: i o to chodzi

Mila: