Funkcja kwadratowa Paulette: 1. Funkcja kwadratowa f(x)= − ¹₄(x+3)(x−5) przyjmuje największą wartość równą: (w odp jest 4, ale ja bym prosiła o obliczenia.) 2. Miejscami zerowymi funkcji kwadratowej f(x)= − 2² + bx −c są liczby 1, oraz −3. Zatem: (w odp jest b+c= −10, ale jak wyżej proszę o obliczenia.)

5-latek: https://matematykaszkolna.pl/strona/3413.html najpierw zapoznaj sie z tym

Paulette: Zapoznałam się z tym, tyle, że mój wynik nie zgadza się z tym, co powinien wyjść.

5-latek: To w takim razie pokaz swoje obliczenia najpierw zadanie nr 1

Ac.: 1. Skoro a = − ¹₄ < 0, to funkcja kwadratowa przyjmuje największą wartość dla x = x_w (w wierzchołku paraboli). x_w to średnia arytmetyczna miejsc zerowych tej funkcji. Oblicz tę współrzędną, a potem oblicz f(x_w) i masz rozwiązane zadanie. 2) Popraw zapis wzoru

Paulette: Po wymnożeniu −x² + 2x +15 = 0 delta = 64 pierw z delty = 8 q = − ⁶⁴₋₄ q = 16

Paulette: W drugim brakuje powinno być: −2x², a reszta jest dobrze

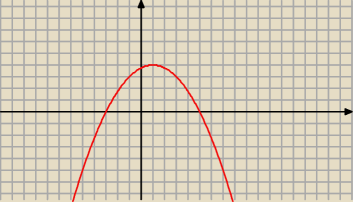
5-latek: A to jest wykres funkcji f(x) do zadania nr 1 .

5-latek:

	1
A przy mnozeniu gdzie poszlo		? na spacer?
	4

Paulette: Przy mnożeniu wyjdą ułamki, w których 4 jest mianownikiem, więc pomnożyłam całe działanie przez 4

Ac.: Już wiesz, co masz źle w 1), a teraz 2): Skoro miejscami zerowymi tej funkcji są liczby 1 oraz −3, to wtedy: f(1) = 0 i f(−3) = 0 −2 * 1² + b * 1 − c = 0 i −2 * (−3)² + b * (−3) − c = 0 Rozwiąż ten układ równań i wtedy oblicz sumę b + c.

Ac.: Jeszcze jedna uwaga co do Twojego rozwiązania: Jak chcesz zrobić swoim sposobem, to musisz przemnożyć też przez −¹₄. Nie możesz potem mnożyć działania przez 4, bo Ty zapisujesz tylko wzór funkcji w innej postaci. Jak piszesz: −x² + 2x + 15 = 0 to wtedy liczysz miejsca zerowe tej funkcji, ale y_w wtedy nie obliczysz poprawnie w ten sposób.

5-latek: Jesli masz taka postac jak ta czyli postac iloczynowa funkcji kwadratowej to takie zadanie liczy sie inaczej . tak jak napisal kolega wyzej . Nie ma potrzeby sprowadzania tego do postaci ogolnej i liczenia delty . Postac iloczynowa jest taka f(x)=a(x−x₁)(x−x₂) . Masz tutaj miejsca zerowqe za darmo x+3=0 to x=−3 i x−5=0 to x=5 . Teraz poparz na ten wykres i zobacz ze tak jest . Masz miejsca zerowe wiec wspolrzedna x_w wierzcholka lezy popsrodku tych miejsc zerowych(czyli jest ich srednia arytmertyczna −to co pisal kolega wyzej )

	x1+x2		−3+5		2
czyli mozemy zapisac ze xw=		wiec u nas xw=		=		=1 i teraz znowqu
	2		2		2

popatrz na wykres czy sie nie zgadza Wiemy ze to funkcja osiaga najwieksza wartosc w wierzcholku ( bo ma ramiona skierowane w dol ) , wiec aby obliczyc ta najwieksza wartosc tej funkcji za x do wzoru podstawiamy wyliczone x_w

	1		1		1
czyli f(x)=−		(xw+3)(xw−5) to f(x)= −		(1+3)(1−5) to f(x)= −		*4*(−4)=
	4		4		4

policz

Paulette: To drugie mi wyszło, ale to pierwsze dalej nie chce wyjść.

Paulette: Dziękuję! Wyszło!

5-latek: Na zdrowie

Ac.: W takim razie spróbuj zrobić to moim sposobem, dokładniej opisał ten sposób wyżej kolega. A ja pokażę Ci, jak powinnaś to zrobić sposobem, którym próbujesz to zrobić Ty. Mamy:

	1		1		1
f(x) = −		(x + 3)(x − 5) = −		(x2 − 5x + 3x − 15) = −		(x2 − 2x − 15) =
	4		4		4

	1		1		15
−		x2 +		x +
	4		2		4

	1		1		15		1		15		16
Δ = (		)2 − 4 * (−		) *		=		+		=		= 4
	2		4		4		4		4		4

	−Δ		−4
yw =		=		= 4
	4a		1   4 * −   4

I wszystko się zgadza.