aa Hugo: Wakacje z Hugusiem Dla jakich wartości parametru m dziedziną funkcji

	3x2−4mx+5
f(x)=
	(m+2)x4+6(m+2)x2+m2

jest zbiór liczb rzeczywistych? Aby dziedziną f był zbiór liczb Rzeczywistych należy się pozbyt 'x' z mianownika Zauważmy w mianowniku: (m+2)x⁴ dla m = −2 wyrażenie się zeruje 6(m+2)x² m = −2 wyrażenie się zeruje Podstawiamy za m = −2 do funkcji

	3x2−4(−2)x+5		3x2+8x+5
f(x)=		=		i dla tej postaci funkcji dziedzina = R
	(−2)2		4

dobrze

Hugo: źle bo jeszcze jak by Δ<0 !

Hugo: o dzięki ! zatem: (m+2)x⁴+6(m+2)x²+m ² zmienna t : = x² (m+2)t²+6(m+2)t+m ² <0 m² + 2m+ 4 − 4(m+2)m²<0 m² +2m +4 −4m³−8m²<0 −4m³ −7m²+2m+4 <0

Kacper: Hugo weź się do roboty

Piotr 10: Hugo Ty wiesz co w ogóle piszesz

Hugo: pośrednio bo dla m = −2 to jest dobre ale także dla delty ujemnej bedzie dziedzina = R zatem trzeba obliczyć delte i mi nie wychodzi i nie rozumiem prosze o pomoc moim sposobem

Kacper: Jak chcesz się pozbyć "x" z mianownika, to ja proponuje go nie pisać i po kłopocie

razor: będzie jeszcze przypadek kiedy Δ > 0 ale pierwiastki są ujemne

Hugo: nie rozumiem razor, mozesz jasniej? jak są pierwiastki ujemne to D = R?

Kacper: No i widać, że niczego nie rozumiesz Mamy w mianowniku wielomian stopnia 4, dlatego liczy się inaczej niż przy wielomianie stopnia 2

Hugo: w(cośtam) = 0 ale tu nic nie pasuje sobie zobacz

Hugo: prosze wytłumaczcie mi to zadanie bo nie rozumiem http://www.zadania.info/d29/665840

Kacper: Popatrzmy ogólnie na zadanie. Mamy wyrażenie

cos
cos innego

Teraz, aby dziedziną był zbiór liczb rzeczywistych potrzeba i wystarcza, aby mianownik nigdy się nie zerował. To przyglądamy się mianownikowi. (m+2)x⁴+6(m+2)x²+m² Chcemy aby wyrażenie to było zawsze różne od 0, dla dowolnej wartości zmiennej x, czyli ⋀_x∊R (m+2)x⁴+6(m+2)x²+m²≠0 (*) Stosujemy podstawienie t=x², t≥0 (m+2)t²+6(m+2)t+m²≠0 (**) Teraz będziemy mieć takie 3 sytuacje: I. Δ_t<0 równanie (**) nie ma rozwiązań, zatem równanie (*) także II. Δ_t=0 równanie (**) ma 1 rozwiązanie, zatem aby równanie (*) nie miało rozwiązań potrzeba by t₀<0 III. Δ_t>0 równanie (**) ma 2 rozwiązania, zatem aby równanie (*) nie miało rozwiązań potrzeba by t₁,t₂<0 załatwiają to wzory Viete'a t₁*t₂>0 t₁+t₂<0 Koniec. Teraz tylko rachunki

Kacper: Oczywiście należy rozpatrzeć warunek m+2=0 Zapomniałem

Kacper: Rozwiązanie, które podałeś jest "trickowe", ale niestosowalne w ogólności.

Hugo: (m+2)t2+6(m+2)t+m2≠0 Δ= m² + 2m + 4 − 4(m+2)m² m² + 2m + 4 − 4m³ − 8m² 4m³ −7m² +2m +4 w(1) = 3 w(2)≠0 w(−2)≠0 w(4)≠0 nie ma z tego pierwiastków wiec nie określe czy Δ >=< 0 vieta:

	m+2
−b/a = t1 + t2 = −		= −1
	(m+2

	m2
c/a = t1 * t2 =		= m
	m+2

Hugo: i co to nam dało

Hugo: edit

m2
	= m2(m+2)
m+2

m=0 v m = −2

Maslanek: Δ=36m²+72m+144−4m³−8m² = −4m³+28m²+72m+144

Maslanek: Ale w zasadzie rozpisywanie tej delty to głupota Δ=36(m+2)²−4m²(m+2)=(m+2)(36m+72−4m²) Dalej prosto

Hugo: sie mi pomineło 6

Maslanek: Co zabawne, nie wiem, gdzie jest błąd U tej z 16:20 m=−2 nie jest pierwiastkiem, a z 16:21 już tak Oczywiście z tej 16:20 Powinno być Δ=36m²+144m+144−4m³−8m² = −4m³+28m²+144m+144

Mila: Hugo, zacznij wreszcie czytać nasze komentarze. 1) w mianowniku masz równanie dwukwadratowe, jeśli m+2≠0. Pierwszy przypadek: m+2=0⇔m=−2 wtedy

	3x2+8x+5
f(x)=		i
	4

D=R dla m=−2 ========== Drugi przypadek: m≠−2 Mianownik : (m+2)x⁴+6(m+2)x²+m² ≠0 (m+2)x⁴+6(m+2)x²+m² =0 aby równanie nie miało rozwiązań, to : Podstawienie: x²=t, t≥0 (m+2)t²+6(m+2)t+m² =0 a) Δ<0 wtedy mianownik nie zeruje się ( rozwiąż warunek ) b) Δ>0 i ( dwa piewiastki są ujemne⇔t₁*t₂>0 i t₁+t₂<0 ( wtedy wyjdzie, że x²<0 a to jest niemożliwe) ( rozwiąż warunek ) Idę na zakupy, wrócę, to sprawdzę Twoje obliczenia.

Hugo: (m+2)(36m+72−4m²) m=−2 v Δ = 36²+72*4*4 = 1296 + 1152=2448 ~49 tak ma wyjść ?

Maslanek: Może reszta warunków daje ładniejszy wynik

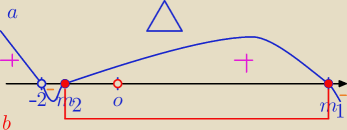
Mila: f(t)=(m+2)t²+6(m+2)t+m² a) m≠0 i Δ<0 Δ=36*(m+2)²−4*m²*(m+2)<0⇔ (m+2)*(36*(m+2)−4m²)<0 (m+2)*(36m+72−4m²)<0 /:4⇔ (m+2)*(−m²+9m+18)<0 Δ_m=81+4*18=81+72=153=9*17 √153=3√17

	−9−3√17		9+3√17
m1=		=		≈[ 10,7]
	−2		2

	9−3√17
m2=		≈[−1,7]
	2

	9−3√17		9+3√17
m∊(−2,		) lub m>		brak miejsc zerowych
	2		2

	9−3√17		9+3√17
b) Δ≥0 ⇔m<−2 lub m∊<		,		>
	2		2

Jeśli Δ=0 to t₁=t₂=−3<0 Ujemne miejsca zerowe f(t)⇔

	−6(m+2)
t1+t2<0⇔		=−6<0 niezależnie od wyboru m≠−2
	m+2

	m2
t1*t2>0⇔		>0⇔m>−2 i m≠0
	m+2

stąd

	9−3√17		9+3√17
m∊<		,0)∪(0,		>
	2		2

Suma warunków m∊<−2,0)∪(0,∞)

Mila: Jeśli nie zrozumiesz to napiszę inne rozwiązanie. Postaraj się przeanalizować.

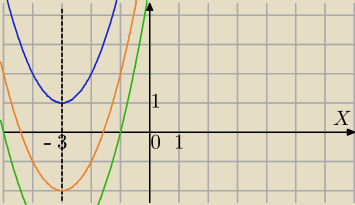
Mila: II sposób 1) m=−2 ⇔D=R to juz ustalone wcześniej 2) m+2≠0 Rozważam równanie po wprowadzeniu zmennej pomocniczej (m+2)t²+6(m+2)t+m²=0 /:(m+2)

	m2
t2+6t +		=0
	m+2

t_w=−3 Takie mogą być wykresy f(t) spróbuj dalej sam.

Hugo: wole I sposób ale dalej nie rozumiem 1. Założenie o pierwiastkach m jest takie że ma być m>0 bo podstawialiśmy pod t:=x² A jeden z m ≈[ 10,7] czyli dodatni ! to czemu odrzucamy 2. m= −2 tez jest ujemny ! a odrzucamy ! 3. Dlaczego miejscem zerowym w wężyku jest 0 4. I to nizej od: "Ujemne miejsca zerowe f(t)" tez nic nie rozumiem

lolo: niektórzy nie będą matematykami...

Mila: Hugo czytaj uważnie wszystko, co napisałam, to zrozumiesz.