Graniastosłup Jacek: Podstawą graniastosłupa prostego jest trójkąt prostokątny o przeciwprostokątnej długości 8 i jednym z kątów 60 stopni. Przez przeciwprostokątną dolnej podstawy i wierzchołek kąta prostego górnej podstawy poprowadzono płaszczyznę. W przekroju otrzymano trójkąt o polu równym 16√3. Oblicz objętość tego graniastosłupa. nie wiem czy dobrze kminię więc proszę o pomoc tutaj co wyskrobałem:

	1
P=		*a*h
	2

	1
16√3=		*8*h
	2

16√3=4h h=4√3

	1
d2=h2−		a2
	2

d²=(4√3)²−4² d²=48−16 d²=32 d=8√2

	H
sin30=
	8√2

1		H
	=
2		8√2

8√2=2h 4√2=h i tutaj moje pytanie co dalej?

Jacek: Ktoś coś ?

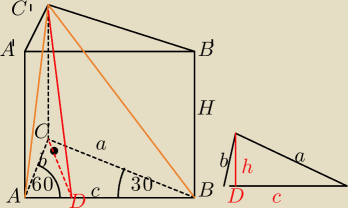
Mila: 1)ΔACB− trójkąt o katach 90,60,30 stopni c=8 b=4 a=4√3

	1		1
PΔABC=		*a*b=		*4*4√3=8√3
	2		2

	1
PΔABC=		*8*h
	2

4h=8√3 h=2√3 ======

	1
P{ΔABC'}=		*c*hp
	2

To dobrze obliczyłeś h_p=4√3 W ΔC'CD z tw. Pitagorasa: h_p²=h²+H² (4√3)²=(2√3)²+H² H=6 V=8√3*6=48√3 ============

Jacek: Dziękuje Milu

Mila: