tRYGONOMETRIA MAJA: Witam, dzisiaj zaczelismy funkcje trygonoemtryczne i mam problem z pewna nierownoscia trygonometryczna.dodam ze ma wyjsc π/12+kπ/3≤x,π/6+kπ/3 a o to nierownosc: tg3x≥1 Na co powinnam zwracac uwage przy rozwiazywaniu tego typu nierownosci?Moglabym prosic o jakas podpowiedz?dziekuje slicznie

Nikka: niech 3x=z tgz ≥ tg^π₄ z wykresu funkcji tg wynika, że tgz>1 dla z∊(^π₄ + kπ, ^π₂ + kπ) czyli ^π₄ + kπ ≤ z ≤ ^π₂ + kπ ^π₄ + kπ ≤ 3x≤ ^π₂ + kπ dzielimy obustronnie przez 3 (chcemy mieć tylko x) ^π₁₂ + ^kπ₃ ≤ x≤ ^π₆ + ^kπ₃ czyli x należy do podanego przez Ciebie przedziału

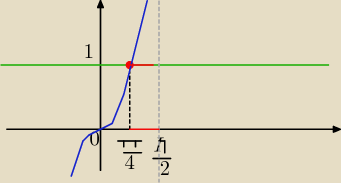
Aza: witam Najprościej rozwiązuje się nierówności patrząc na wykresy założ x ≠^π₂ y = tgx i y = tg^π₄= 1 tg3x ≥1 => tg3x ≥tg^π₄ widać , gdzie niebieski wykres ( tg3x) jest nad zielonym wykresem tg^π₄ zatem dla I. ćw. x€< ^π₄, ^π₂) bo x ≠^π₂ więc 3x ≥ ^π₄ + k*π i 3x < ^π₂ +k*π , k€C dzieląc przez 3 otrzymasz x ≥ ^π₁₂+k*^π₃ i x < ^π₆+ k*^π₃ odp: x€ < ^π₁₂+k*^π₃ , ^π₆ + k*^π₃ )

Aza: Nikka , przedział musi być prawostronnie otwarty bo x ≠ ^π₂ dla tgx

Nikka: tak, tak, dla π/2 tg nie istnieje