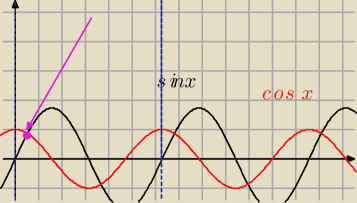
aa Hugo: Znajdź najmniejszą i największą wartość funkcji f(x) = √3sinx + cos x w przedziale <0 ;2π>. f(x) = √3sinx + cos x Zabrałbym się za to tak: że policzył bym dla wierzchołków sin i cos wartości tej funkcji. wierzchołek sin pada w pi/2 czyli to co mnie świeżo MILA i RAZOR nauczyli:

	π		π		π
f(		)= √3sin		+ cos
	2		2		2

= 1 * √3 + 0 = √3 dla wierzchołka cosinusa f(0)= 0 + 1 =1 Jeszcze nie wiem co z tym fioletowym pkt gdyby

Maslanek: Prościej

	√3		1		pi		pi
Zauważ, że √3sinx+cosx = 2*(		sinx+		cosx) = 2*(sin		sinx+cos		cosx)
	2		2		3		3

=

	pi
= 2*cos(x−		)
	3

Maslanek: Ewentualnie wykorzystać rachunek różniczkowy do tego

Kacper: Nie dodajemy wartości na "piechotę". Metoda błędna

Hugo: a z jakiego to jest wzoru

Maslanek: Cosinus różnicy kątów

Kacper: Maślanek zastosował wzór sin(α+β)=sinα*cosβ+cosα*sinβ W zasadzie to inny ale ten można

Hugo: no dobrze a jak przeszedłeś z linijki 2(sin pi/3sin x + cos pi/3 cosx) do linijki 2cos(x− pi/3)

Maslanek: Cosinus różnicy kątów

Hugo: okej a w takim razie jak przeszedleś z tego jedno wyzej 2(√3/2 sin x + 1/2 cosx) ==========> 2(sin pi/3 sinx + cos pi/3 cosx)

Mila: Do 21:33. cos(α−β)=cosα *cosβ+sinα*sinβ

	π
α=
	3

β=x Wzór stosujesz od prawej do lewej. Mamy

	1		√3		π		π
2*(		*cosx+		*sinx)=2 cos(		−x)=2cos(x−		)
	2		2		3		3

Kacper inny wzór stosuje .

	π
f(x)=2cos(x−		)
	3

	π
−1≤cos(x−		)≤1 /*2
	3

	π
−2≤2cos(x−		)≤2
	3

Z_w=<−2,2>

Hugo: Ponownie wam dzięuję i to moje tez mi sie wyjasnilo

Hugo: A Mila to zadanie co wczoraj kacper wrzucił z planimetri próbowała ?

Mila: Zostawiam to dla młodych orłów.

Hugo: Mila przecież także należysz do młodego pokolenia ! stary to jest Pitagoras i Tależ