aa Hugo: rozwiąz równanie w √3cos x = 1+ sin x w przedziale <0, 2pi> . √3cos x = 1+ sinx 1 = sinx − √3cosx /² 1= (sinx− √3cosx)² 1= sin²x − 2√3sinxcosx + 3cos²x 1= sin²x − 2√3sinxcosx + 3cos²x 1= sin²x +cos²x +2cos²x − 2√3sinxcosx 1=1+2cos²x − 2√3sin2x 0= 2(1−sin²x) −2√3sin2x 0=2 − 2sin²x − 2√3sin2x /:2 1 − sin²x − √3sin2x = 0 i czo dalej

Hugo: pod czerwonym mam źle bo źle złożyłem do sin2x 1=1+2cos²x − √3sin2x 0= 2(1−sin²x) −√3sin2x 0=2 − 2sin²x − √3sin2x − 2sin²x − √3sin2x + 2 = 0

razor: A to można tak podnosić równanie do kwadratu bez założeń? Prościej będzie tak √3cosx = 1+sinx | ()² 3cos²x = 1+2sinx+sin²x 3(1−sin²x) = 1+2sinx+sin²x 4sin²x+2sinx−2 = 0 oczywiście przy odpowiednich założeniach

Hugo: jakich założeniach no prosciej 4sin²x+2sinx−2 = 0 4t² + 2t −2 =0 2t² +t −1=0 Δ= 1+8 = 9 t₁= −1−3/4 v t₂=−1+3/4 t₁= − 1 v t₂ = 0,5 sinx = −1 v sin x = 0,5

	π		5π
x = 3/2 pi v		v
	6		6

razor: 1 = −1 | ()² 1 = 1 hmm

	5π
podstaw		do pierwszego równania i zobacz co się stanie
	6

Hugo: to jest z matury zadanie i wlaśnie na tym przykładzie chce sie nauczyc czy coś; naucz mnie kiedy sie wlasnie odejmuje te rozwiązania Jaka jest zasada? z tą odpadanką

Mila: I sposób √3 cosx−sinx=1 /:2

√3		1		1
	*cosx−		*sinx=		⇔
2		2		2

	π		π		1
sin		*cosx−cos		*sinx=		⇔Korzystam z wzoru sin(α−β)=...
	3		3		2

	π		1
sin(		−x)=		i x∊<0,2π>⇔
	3		2

π		π		π		5π
	−x=		+2kπ lub		−x=		+2kπ i x∊<0,2π>
3		6		3		6

	π		−π
x=		−2kπ lub x=		−2kπ
	6		2

Podstawiam k=0

	π		π
x=		∊<0,2π> lub x=−		∉<0,2π>
	6		2

Podstawiam k=−1

	π		π		3π
x=		+2π∉<0,2π> lub x=−		+2π=		∊<0,2π>
	6		2		2

odp.

	π		3π
x∊{		,		}
	6		2

==================

Hugo: no Dobrze Milo dziękuję, ale nie o to sie dokońca rozchodzi @Razor: czyli przez to że podnosiliśmy do kwadratu sie kasuje 1 rozw a takto wszystko

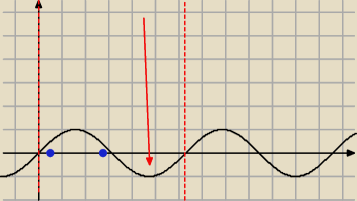
Hugo: A jak moge podstawić do 1 równania 5/6 pi √3cos x = 1+ sin x

Hugo: bo na chłopski rozum <myśli> 1 = (cośtam)² 1= cośtam² i potem było u mnie: x = 3/2 pi v x = 5/6 pi v x=1/6pi sinx = 0,5 i tu mamy prawda: x = pi/6 lub 5/6 i to drugie odpada ale no... jak to dowieźć że to akurat wykasować i jak podstawić

Mila: No, niezupełnie masz rację, Twoje kombinacje są ryzykowne.

	5π		3
L=√3*cos		=√3*(−√3}{2}=−
	6		2

	5π		1
P=1+sin		=1+
	6		2

L≠P

Hugo: ooo to tak sie to podstawia dziekuje ! Milo dziś miałem siódmą godzię korypetycji i chodź na forum to nie wygląda bardzo sb radzę w tłumaczeniu zadań mojemu uczniowi !

Kacper: Hugo daje korki?

Hugo: Melchiorowi i Baltazarowi a czo

Hugo: Podobno należy robić to co sie lubi bezwzględu na konsekwencje. Życie jest po to by być szczęślliwym

Kacper: I oni cie słuchają?

bezendu: Kacper wejdź na gadu

Kacper: już

Hugo: Huguś jest świetnym mówcą i uwielbia malować