Matura Blue: Ostatnie zadanko z tej maturki, z który nie umiem sobie poradzić: Dany jest trójkąt o bokach 5, 8, 12. Dwusieczna największego kąta wewnętrznego tego trójkąta dzieli jeden z jego boków na dwa odcinki. Wyznacz długości tych odcinków. Coś tutaj kombinowałam z tw. cosinusów, ale nie wychodziło... Pomożecie?

Kacper: Znasz twierdzenie o dwusiecznej? http://pl.wikipedia.org/wiki/Twierdzenie_o_dwusiecznej_k%C4%85ta_wewn%C4%99trznego_w_tr%C3%B3jk%C4%85cie Wystarczy podstawić

Blue: O kurcze, było coś takiego? Jakoś sobie nie przypominam, heh xD A jest to może w karcie wzorów? ^^

52: Tego w karcie wzorów nie ma, z tego co kojarzę...

Blue: Ech szkoda, że nie ma.. Ale w każdym razie dzięki Kacper !

5-latek: Ale to jest jedno z podstawowych twierdzen wiec powinnas je znac na pamiec . Poza tym w ksiazce jest wytlumaczone .

Kacper: Proszę bardzo Prosty dowód robi się z twierdzenia sinusów

daras: https://www.youtube.com/watch?v=FJ5q1z9xB0g

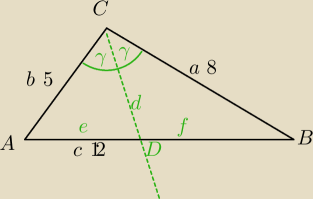
Mila: CD^→− dwusieczna kąta wewnętrznego C

PΔADC		e
	=		− Δmają wspólną wysokość opuszczoną na AB z wierzchołka C.⇔
PΔBDC		f

0,5b*d*sinγ		e
	=		⇔
0,5a*d*sinγ		f

b		e
	=		tw. o dwusiecznej kąta wewnętrznego Δ, można zapisać inaczej, np.
a		f

b		a
	=
e		f

W zadaniu wykorzystasz jeszcze, że : e+f=12 i koniec problemu.

pigor: ..., niech x i 12−x szukane długości odcinków, to z tw. o dwusiecznej np. ⁵_x= ⁸_12−x i 0<x<12 ⇒ 8x=60−5x ⇔ 13x=60 ⇔ x= ⁶⁰₁₃=4⁸₁₃,

Mila: A Blue odpuściła ważny temat.