rachunekzbiorwoo zombi: niech

	1
An = [(−1)n, 1+		], gdzie n∊N+
	n

Wyznaczyć ∪_n=1^∞A_n oraz ∩_n=1^∞A_n Jak uargumentować, to że ∪_n=1^∞A_n = <−1,2> i ∩_n=1^∞A_n = {1}

	1
Wiemy, że (−1)n = ±1 w zależności od n, natomiast 1+		∊ (1,2>
	n

Kurczę to się wydaje mega oczywiste, jak miałbym to komuś wytłumaczyć, tak formalnie?

WueR: Ale A_n to chyba zbior? Wiec powinny byc nawiasy klamrowe. Zbiory A, B sa rowne, o ile zachodzi: A⊂B i B⊂A.

zombi:

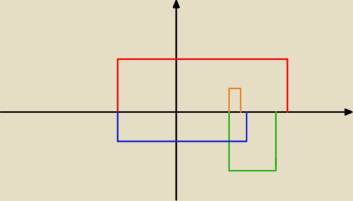
	1
Tu raczej chodzi o zbiór punktów od (−1)n do 1+		takie kolejne przedziały na osi, coś w
	n

ten deseń kolejno dla n = 1, 2, 3, 4

WueR: Tak, moja pomylka, z rozpedu przeczytalem [(−1)ⁿ: n∊N]. Czyli jest dobrze i A_n to przedzial domkniety. Co nie zmienia faktu, ze trzeba pokazac dwa zawierania.

Maslanek: Jeżeli chodzi o sumę: [−1,2] I zawieranie się tego przedziału w sumie jest oczywiste. [−1,2]⊂∪A_n, bo dla n=1 mamy A₁=[−1,2] Zawieranie ∪A_n⊂[−1,2] Zauważmy, że dla n parzystego (oznaczmy np) mamy A_np⊂[1,2] Co się dzieje dla n nieparzystego? Twierdzimy, że ∪A_n⊂[−1,2].

	1
Dla n nieparzystych, tj. postaci n=2k−1; k∊N mamy A2k−1=[−1,1+		]
	2k−1

Weźmy więc dowolne k₀. Pokażemy, że ciąg zbiorów postaci A_2k−1 jest zstępujący, tj. A_2k+1⊂A_2k−1.

	1		1		1		1
Oczywiście		<		, zatem 1+		<1+		.
	2k0+1		2k0−1		2k0+1		2k0−1

Jednocześnie lewy kraniec zbioru jest stały dla dowolnego k₀. Czyli ciąg jest zstępujący oraz najwiekszy przedział znajdziemy dla k=1.

Maslanek: Jeżeli chodzi o iloczyn. 1) Zawieranie iloczynu w każdym zbiorze jest trywialne, 2) * Zauważyć, że iloczyn lewego krańca wszystkich zbiorów jest równy 1, * Zauważyć, że prawy kraniec zbiorów (ozn. g) jest ciągiem ograniczonym z dołu przez 1. Pokazać, że dla każdego k₀ g>1 oraz, że dla dowolnego k₀ istnieje k₁ takie, że g_k1<g_k0, tj. ciąg jest ściśle malejący do 1. Wtedy z tw. o ciągu monotoniczym i ograniczonym mamy, że granica jest równa 1. Stąd też wynika zawieranie.

WueR: No, ale skoro zombi chcial formalnie, to napisanie, ze przeciez "to widac" nie wystarczy i co jak co, ale trzeba pokazac wynikanie: x∊∪_n=1^∞A_n ⇒ x ∊ [−1, 2].

zombi: Noo o to mi chodziło Jak miałbym to komuś wytłumaczyć. Dzięki wielkie za pomoc.

WueR: Ja bym zrobil tak dla sumy: (⊂) [czyli z definicji inkluzji pokazujemy, ze zachodzi: ∀x: x∊U_n=1^∞ ⇒ x ∊ [−1,2] ] Ustalmy dowolnie x taki, ze x∊U_n=1^∞, wobec czego istnieje n_x∊N takie, ze x ∊ A_nx.

	1
Zatem (−1)nx ≤ x ≤ 1 +		. Ale dla dowolnego nx mamy:w −1 ≤ (−1)nx, z czego
	nx

wynika, ze −1 ≤ x. Po drugie, dla dowolnego n_x∊N mamy:

	1		1		1
1 ≥ 0 ⇔ nx+1 ≥ nx ⇔		≤		, skad wynika, ze 1+		≤ A1 = 2, wiec
	nx+1		nx		nx

rowniez x ≤ 2. Ostatecznie otrzymujemy, ze −1 ≤ x ≤ 2, a wobec dowolnosci wyboru x stwierdzamy prawdziwosc tezy.

WueR: Hmm, w jednym miejscu pewna niescislosc.

	1		1
Mialo byc: 1+		≤ 1+		= 2 [A1 tam nie powinno byc, bo to by byly czyste herezje].
	nx		1

Maslanek: Już dawno nie widziałem takich dowodów Ładny Miło było znowu przeczytać coś takiego

zombi: Właśnie o coś takiego mi chodziło, bo w domu jak się uczę to za bardzo nie mam pojęcia jak to wszystko formalnie zapisywać, więc muszę się na czymś opierać. Dzięki wielkie panowie!

zombi: A coś do teorii rachunku zbiorów polecacie? Jakaś stronka ew. książka?

WueR: Wazne, zeby takich "oczywistosci" nie pomijac, bo to nie jest trudne, ale trzeba umiec mimo wszystko, a wlasnie jak sie samemu uczy, to mozna nie wiedziec, jak do konca powinno to wygladac. Wiec dobrze, ze pytasz i tak trzymaj.

WueR: Ja nic polecic nie moge, bo wiedze na ten temat czerpalem jedynie z wykladow.

zombi: Okej, to weźmy taki przykład z wikipedii

	1		1
Niech An = (1−		, 1+		)
	n+1		n+1

	1		1
Oznaczmy przez an = 1−		oraz przez bn = 1+
	n+1		n+1

Weźmy pod lupę a_n.

	−1
Zauważmy, że an − an+1 = (po przekształceniach)		< 0 dla każdego n∊N,
	(n+1)(n+2)

	1
wobec tego an+1 > an a tym bardziej an ≥ inf(an) = a1 =		.
	2

	1
Następnie weźmy bn. Analogicznie bn−bn+1 =		> 0, wobec tego dla każdego
	(n+1)(n+2)

n∊N zachodzi

	3
bn > bn+1 a tym bardziej bn+1 < bn ≤ sup(bn) = b1 =
	2

	1		3
Wobec tego dla każdego n∊N, An⊆A1, czyli ∪n=1∞ = [		,		]
	2		2

I teraz pytanie jeśli chodzi o iloczyn, czy takie uzasadnienie jest ok?

	1
an = 1 −		→ 1, ponadto an+1 > an, czyli sup(an) ≤ 1
	n+1

	1
bn = 1 +		→ 1, oraz bn+1 < bn, czyli inf(bn) ≥ 1
	n+1

ponadto zachodzi a_n < b_n, zatem dla każdego n∊N, mamy ∩_n=1^∞A_n = {1} Pytanko ekstra czy można zapisać tak (korzystając ze wcześniejszych wypocin)

	1		1
1−		≤ An ≤ 1+		przechodząc w ∞ z tw. o 3 ciągach mamy An→1 czy nie moge tak
	n+1		n+1

przy zbiorach?

Maslanek: A_n → 1 wskazuje, że ciąg dąży do LICZBY 1. Ale A_n jest zbiorem, nie zaś ciągiem, i jest zbieżny do ZBIORU: {1} w nieskończoności.

Maslanek: Głupoty popisałem A_n jest ciągiem zbiorów, nie zaś ciągiem liczbowym

zombi: Tak tylko zapytałem A reszta wyżej spoko w miarę?

Maslanek: Albo... trzymając się oznaczeń: A_n − zbiór (A_n) − ciąg (A_n) → {1}

zombi: Ale to co wyżej pokazałem jest okej? W tym rozumowaniu?

zombi: Dobra jeszcze taki przykład: Niech A_t = {x∊R: xt ≤ 2} dla t∊(−∞,0) ∪ (0,+∞) Wyznacz U_t∊R\{0}A_t oraz ∩_t∊R\{0}A_t Podpowiedź jest taka, żeby rozdzielić t na dwa przedziały (I^o t>0 i II^o t<0) Suma

	2		2
Io t>0, wobec tego xt ≤ 2 ⇔ x≤		, ponadto		∊(0, +∞) wobec tego x∊R, przypadek II
	t		t

	2		2
analogicznie z tym, że		∊(−∞, 0) oraz x≥		, wniosek ten sam x∊R, czyli
	t		t

U_t∊R\{0}A_t = R∪R = R. Iloczyn

	2		2
Io t>0, zauważamy, że 0 < inf(		) ≤		, wobec tego ∩t>0At = (−∞, 0]
	t		t

	2		2		2
analogicznie drugi przypadek, z tym, że x≥		oraz 0 > sup(		≥		, zatem
	t		t		t

∩_t<0A_t = [0,+∞] Czyli ∩A_t = {0}

zombi: W Banasiu taki rozwiązanie, bardziej skrótowe http://i.snag.gy/3pYDF.jpg

zombi: Mógłby ktoś skontrolować te moje dwa przykłady? Bo serio chce się oswoić z tą dokładnością zapisu już teraz żebym później miał łatwiej.

zombi: http://snag.gy/DzZkN.jpg Weźmy na to przykład a), mogę go indukcyjnie z wykorzystaniem zaprzeczenia alternatywy de Morgana?

5-latek: Ja CI w tym nie pomoge ale moze zapytaj sie Pana dr Jana Kraszewskiego z Uniwesytetu Wroclawskiego On wydal ksiazke Wstep do matematyki B. Ja go zapytalem niedawno o pewna ksiazke i nie zostawil to bez odpowiedzi . Wiec moze Ty tez sprobuj .

zombi: Mam ją i tam jest ten przykład tylko jakoś dziwnie wytłumaczony.

5-latek: To ja bym tym bardziej zapytal .

Kacper: Ja tego nie lubię i przykro mi, ale nie jestem w stanie pomóc

Godzio: To się liczy może na jednych zajęciach, a później na kolokwium, tyle z tym przygody

WueR: Indukcyjnie, tzn za pomoca indukcji matematycznej? Ale tam wskazniki nie sa naturalne tylko ze zbioru T.

Kacper: Godzio dlatego po 5 latach nawet tego nie pamiętam

WueR: To chyba tak powinno wygladac (ja tez nie do konca pamietam wszystko): x∊(∪_t∊TA_t)' ⇔ ¬ x∊∪_t∊TA_t ⇔ ¬[∃t∊T: x∊A_t] ⇔ ∀t∊T: x∉A_t ⇔ ∀t∊T: x∊A_t' ⇔ x∊ ∩_t∊TA_t'

WueR: Zauwaz, ze tutaj tez jest pokazana rownosc dwoch zbiorow, bo pamietajac, ze rownowaznosc to dwie implikacje pokazujemy najpierw zawieranie ⊂, a pozniej ⊃.

zombi: Mi też się to zbytnio nie podoba, ale chce przez to przebrnąć jakoś

Kacper: WueR jak dla mnie to twoje jest ok

Maslanek: b) od prawej strony zaczynając: x∊∪A_t' ⇔ istnieje t∊T x∊A_t' ⇔ istnieje t∊T ~(x∊A_t) ⇔ istnieje t∊T x∉A_t ⇔ ~ (~ istnieje t∊T x∉A_t) ⇔ ~ (dla wszystkich t∊T x∊A_t) ⇔ ~ (x∊∩A_t) ⇔ (x∊∩A_t)'