 Ktoś mógłby mi to łopatologicznie wytłumaczyć
Ktoś mógłby mi to łopatologicznie wytłumaczyć To jest parabola z ramionami do góry.
Pierwiastki są takie
x1−2m−1=0 x1=2m+1
x2=m
tutaj http://www.matematyka.pl/205511.htm jest takie wytłumaczenie, ale go nie rozumiem.
"(...) mamy 2m+1=x1 oraz x2=m.
Gdy 2m+1>m czyli gdy m>−1 to mniejszy pierwiastek musi być mniejszy lub równy jeden: m ≤ 1
a większy pierwiastek musi być większy lub równy 2:
To jest parabola z ramionami do góry.
Pierwiastki są takie
x1−2m−1=0 x1=2m+1
x2=m
tutaj http://www.matematyka.pl/205511.htm jest takie wytłumaczenie, ale go nie rozumiem.
"(...) mamy 2m+1=x1 oraz x2=m.
Gdy 2m+1>m czyli gdy m>−1 to mniejszy pierwiastek musi być mniejszy lub równy jeden: m ≤ 1
a większy pierwiastek musi być większy lub równy 2:
| 1 | ||
2m+1 ≥ 2, rozwiązaniem w/w nierówności jest przedział < | ,1>. | |
| 2 |
| 1 | ||
( | ,1). " | |
| 2 |

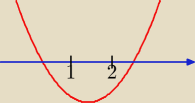 To jest ta sytuacja
To jest ta sytuacja
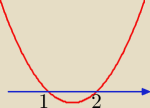 A to druga sytuacja, gdymo to 1 i 2
A to druga sytuacja, gdymo to 1 i 2
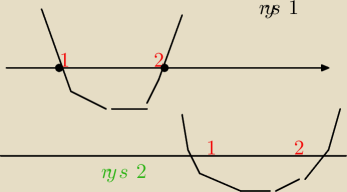 czyli wynika, że to rysunek 1 to f(1)=0 i f(2) =0
rys. 2 to f(1)<0, bo wykres dla x=1 jest pod OX,
f(2)<0 bo wykres dla x=1 jest pod OX,
Tylko ja właśnie myślałem, że jeśli jest zapis "każdą liczbę rzeczywistą należącą do przedziału
<1,2>"
to właśnie miejsce zerowe ma być większe/równe od 1, a drugie miejsce zerowe ma być mniejsze/
równe od 2. W poście podanym w linku autor pisze, że "Z warunków wynika, że jedno miejsce
zerowe musi być mniejsze lub równe od 1, a drugie większe lub równe od 2".
No i tu chyba mylę miejsca zerowe z każdą liczbę rzeczywistą należącą do przedziału <1,2>
czyli wynika, że to rysunek 1 to f(1)=0 i f(2) =0
rys. 2 to f(1)<0, bo wykres dla x=1 jest pod OX,
f(2)<0 bo wykres dla x=1 jest pod OX,
Tylko ja właśnie myślałem, że jeśli jest zapis "każdą liczbę rzeczywistą należącą do przedziału
<1,2>"
to właśnie miejsce zerowe ma być większe/równe od 1, a drugie miejsce zerowe ma być mniejsze/
równe od 2. W poście podanym w linku autor pisze, że "Z warunków wynika, że jedno miejsce
zerowe musi być mniejsze lub równe od 1, a drugie większe lub równe od 2".
No i tu chyba mylę miejsca zerowe z każdą liczbę rzeczywistą należącą do przedziału <1,2>

 ? Chyba łatwiejszy jest do zrozumienia. A tak PS: jeśli
chcesz narysować ''uśmiechniętą buźkę'' to z boku masz y=.. Wystarczy tam wpisać x2 i gotowe
? Chyba łatwiejszy jest do zrozumienia. A tak PS: jeśli
chcesz narysować ''uśmiechniętą buźkę'' to z boku masz y=.. Wystarczy tam wpisać x2 i gotowe



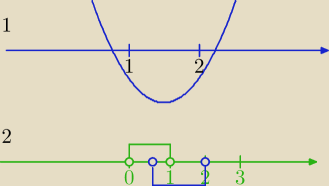 Parabola jest skierowana do góry. rys.(1)
f(x)=(x−2m−1)*(x−m)
f(1)<0 i f(2)<0
1) f(1)=(1−2m−1)*(1−m)
(−2m)*(1−m)<0⇔m∊(0,1)
i
2) f(2)<0
f(2)=(2−2m−1)*(2−m)
(1−2m)*(2−m)<0
Parabola jest skierowana do góry. rys.(1)
f(x)=(x−2m−1)*(x−m)
f(1)<0 i f(2)<0
1) f(1)=(1−2m−1)*(1−m)
(−2m)*(1−m)<0⇔m∊(0,1)
i
2) f(2)<0
f(2)=(2−2m−1)*(2−m)
(1−2m)*(2−m)<0
| 1 | ||
dla m∊( | ,1) spełniona jest nierówność (x−2m−1)*(x−m)<0 dla x∊<1,2> | |
| 2 |
| 1 | ||
m<1 i m> | ⇔ | |
| 2 |
| 1 | ||
m∊( | ,1) | |
| 2 |
 Dziękuję Mila.
Czyli w pierwszym kroku sprawdzasz, dla jakich m obie nierówność są prawdziwe. Robiłem coś w
tym kierunku, ale nie wpadłem na to, że trzeba ustalić część wspólną, więc uznałem, że zły
wynik i tą metodę sobie odpuściłem.
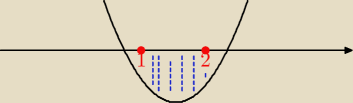
Chyba zaczynam rozumieć to zadanie. Czy stwierdzenie, że "nierówność (x−2m−1)(x−m)<0 jest
spełniona przez każdą liczbę rzeczywistą należącą do przedziału <1,2> " oznacza, że w
przedziale <1,2> wykres musi być pod osią OX
Dziękuję Mila.
Czyli w pierwszym kroku sprawdzasz, dla jakich m obie nierówność są prawdziwe. Robiłem coś w
tym kierunku, ale nie wpadłem na to, że trzeba ustalić część wspólną, więc uznałem, że zły
wynik i tą metodę sobie odpuściłem.
Chyba zaczynam rozumieć to zadanie. Czy stwierdzenie, że "nierówność (x−2m−1)(x−m)<0 jest
spełniona przez każdą liczbę rzeczywistą należącą do przedziału <1,2> " oznacza, że w
przedziale <1,2> wykres musi być pod osią OX  Czyli szukam m, dla których funkcja kwadratowa
w przedziale <1,2> jest ujemna dla każdej wartości x. Jeśli tak, to wtedy jest wykres taki jak
to narysowałaś.
Czyli szukam m, dla których funkcja kwadratowa
w przedziale <1,2> jest ujemna dla każdej wartości x. Jeśli tak, to wtedy jest wykres taki jak
to narysowałaś.
